|
GR9677 #57
|
|
|
|
|
Alternate Solutions |
scottopoly
2006-11-03 19:39:18 | Use Raleigh's criterion! |  |
|
|
Comments |
faith
2010-11-11 19:33:52 | id like to also point out.
no need to convert radian to degree. if u do so, u have to use sin teta and... its impossible to get the value without memorising the sin table.
unlike me.. i did this with a calculator. hahar.. |  | gman
2010-11-10 18:20:37 | Just to clarify...
 = m \lambda) with integer, non-zero with integer, non-zero 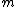 giving successive minima. giving successive minima.
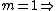 first minimum. first minimum.
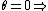 central maximum. central maximum.
So 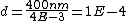
scasplte2
2011-09-01 18:59:14 |
This made it so much clearer to me... thank you
|
sina2
2013-09-30 00:28:24 |
Better answer.
|
|  | azureblue22
2010-11-05 21:33:36 | For all you guys who disagree about the factor of two I have your answer.
There is also a factor of two hidden in the distance 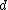 , allow me to explain.rnrnFor single slit diffraction the diffraction pattern emerges. because the photons interfere with each other as they pass through the single slit. For a minimum to occur each photon must be , allow me to explain.rnrnFor single slit diffraction the diffraction pattern emerges. because the photons interfere with each other as they pass through the single slit. For a minimum to occur each photon must be  radians out of phase with another photon passing through the slit. One way to count the out of phase pairs is to divide the slit in two at radians out of phase with another photon passing through the slit. One way to count the out of phase pairs is to divide the slit in two at 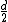 . Pair the photon at the very bottom of the slit with the photon in the middle of the slit, then think of these two locations as two separate, infinitesimally small slits. Wa-lah! Were back to the double slit pattern! Now move the single slit very far away from the basement wall where you measured the double slit pattern in undergraduate lab. The slit becomes a point and you get familiar results. And look on the bright side, you are never going to see that wall again because you're going off to grad school. Good luck. . Pair the photon at the very bottom of the slit with the photon in the middle of the slit, then think of these two locations as two separate, infinitesimally small slits. Wa-lah! Were back to the double slit pattern! Now move the single slit very far away from the basement wall where you measured the double slit pattern in undergraduate lab. The slit becomes a point and you get familiar results. And look on the bright side, you are never going to see that wall again because you're going off to grad school. Good luck.
P.S. So you see, the formula becomes: 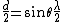 . . |  | azureblue22
2010-11-05 21:32:23 | For all you guys who disagree about the factor of two I have your answer. There is also a factor of two hidden in the distance 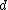 , allow me to explain.rnrnFor single slit diffraction the diffraction pattern emerges. because the photons interfere with each other as they pass through the single slit. For a minimum to occur each photon must be , allow me to explain.rnrnFor single slit diffraction the diffraction pattern emerges. because the photons interfere with each other as they pass through the single slit. For a minimum to occur each photon must be  radians out of phase with another photon passing through the slit. One way to count the out of phase pairs is to divide the slit in two at radians out of phase with another photon passing through the slit. One way to count the out of phase pairs is to divide the slit in two at 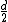 . Pair the photon at the very bottom of the slit with the photon in the middle of the slit, then think of these two locations as two separate, infinitesimally small slits. Wa-lah! Were back to the double slit pattern! Now move the single slit very far away from the basement wall where you measured the double slit pattern in undergraduate lab. The slit becomes a point and you get familiar results. And look on the bright side, you are never going to see that wall again because you're going off to grad school. Good luck. rnrnP.S. So you see, the formula becomes: . Pair the photon at the very bottom of the slit with the photon in the middle of the slit, then think of these two locations as two separate, infinitesimally small slits. Wa-lah! Were back to the double slit pattern! Now move the single slit very far away from the basement wall where you measured the double slit pattern in undergraduate lab. The slit becomes a point and you get familiar results. And look on the bright side, you are never going to see that wall again because you're going off to grad school. Good luck. rnrnP.S. So you see, the formula becomes: 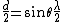 . . |  | mianghazanfar786
2010-07-20 18:17:20 | There is a confusion that "one has integer m for maxima and half-integers for minima. (Opposite to single-slit interference.)"
We should use directly for diffraction pattern,
1 for minima and 1/2 for maxima so we use m=1
to solve the question by Bragg's Diffraction law |  | archard
2010-05-30 13:20:12 | If all you knew was that minima occur at half integers, you could make a wild guess by noticing that C and D differ by a factor of a half, and since ETS is always trying to trick you it's probably one of the two, and most likely C because 1 is half of 2. |  | sullx
2009-11-02 18:39:02 | Careful! The value 'm' corresponds to Minimum for single slit diffraction, and maximum for double slit interference.
Yosun: "The single slit diffraction formula is d \sin \theta = \lambda m, where one has integer m for maxima and half-integers for minima. (Opposite to single-slit interference.) "
niux
2009-11-05 14:15:02 |
Gee. Seems Yosun using different semantics?. I agree with RootMeanSquare explanation, and for single slit, m should tell the number of minima you are dealing with.
|
|  | tan
2009-10-23 23:09:13 | Central maximum occurs at 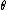 = 0 = 0
First minimum occurs at d sin 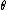 = =  /2 /2
Answer should be 5 x 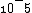 . .
What's wrong? |  | boundforthefloor
2006-11-24 23:43:14 | Wolfram explains this well giving minima at  = m\lambda/d) and the primary maxima at 0. and the primary maxima at 0.
see:
http://scienceworld.wolfram.com/physics/FraunhoferDiffractionSingleSlit.html
physicsisgod
2008-10-29 22:12:18 |
Yea, you can think of it like the center max is actually at 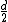 , and then the optical path difference between a ray diffracted at an angle , and then the optical path difference between a ray diffracted at an angle 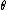 at the center ( at the center (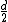 ), and one at 0, is ), and one at 0, is 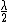 if there's a minimum (destructive inteference), and that has to be equal to if there's a minimum (destructive inteference), and that has to be equal to 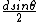 . .
|
|  | RootMeanSquare
2006-11-24 14:31:54 | Okay, I'll never remember that I don't have to log in before posting...
Anyway: It seems here is a little confusion about the factor 2. 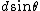 gives you the optical retardation between waves originating a distance d apart within the slit. For a full minimum, you need to find a pair of beams that cancel each other out for every point within the slit, i.e. you actually need a optical retardation of gives you the optical retardation between waves originating a distance d apart within the slit. For a full minimum, you need to find a pair of beams that cancel each other out for every point within the slit, i.e. you actually need a optical retardation of 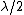 for point for point 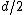 apart. Hence you end up with apart. Hence you end up with 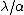 as the width of the slit. as the width of the slit.
mhas035
2007-03-25 21:54:27 |
Thanks! Some clarity!
|
|  | RootMeanSquare
2006-11-24 14:25:50 | |  | scottopoly
2006-11-03 19:39:18 | Use Raleigh's criterion!
physicsisgod
2008-10-29 22:04:35 |
For those of you who are not as enlightened as our fortunate friend scottopoly, Raleigh's Criterion is a formula for deriving the distance between two point sources necessary to resolve them, given their angular separation, 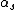 , and the wavelength of emitted light, , and the wavelength of emitted light,  . The formula is . The formula is
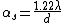
But Raleigh's Criterion only applies for a circular slit, thus the factor of 1.22. If you just use the regular old equation for the distance between the center maximum and the first minimum given a single slit diffraction,
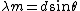 , ,
and the small angle approximation, you'll derive the same formula without the 1.22 factor
Source: http://www.ux1.eiu.edu/~cfadd/3050/Ch20WO/OpRes.html
|
apr2010
2010-04-06 14:20:00 |
Very nice, also makes me remembering the raileigh criterion!
|
|  | buddy.epson
2006-10-13 16:01:42 | Re: Previous User Comment
For single slit diffraction, m corresponds to the center of the dark band (minima). For multiple slits and x-ray diffraction, it corresponds to the center of the bright bands (maxima). The posted solution is correct.
pablojm
2006-10-28 14:39:50 |
In fact, nahmad is right and the problem is incorrectly worded. You can check in any optics book that the formula for minima is d(theta)=m(lambda), where m is a half-integer. Plugging in m=0 and the given values for (lambda) and (theta), you get answer B. The mistake in the original solution is that you stated that m should be a half-integer for minima, and then you plugged in m=1.
Cheers,
Pablo
|
f4hy
2009-04-03 17:37:10 |
The problem states angle between the first minimum and the central max. Not the angle between two mins.
|
|  | nahmad
2006-03-31 22:40:22 | I don't understand. The problems gives the angle between the first minimum and the central max. Doesn't that correspond to m=1/2 which leads to d = 5 x 10^-5 which is B?
suyq
2010-11-07 19:59:33 |
I think B is the right answer!
|
nimesh.nic
2011-11-01 01:20:14 |
I think this is the right ans ...please someone explain .....
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
