|
GR9677 #58
|
|
|
Problem
|
|
|
This problem is still being typed. |
Optics }Lensmaker Equations }Lensmaker Equations
Although this problem mentions lasers, no knowledge of quantum mechanics or even lasers is required. Instead, the problem can be solved as a simple geometric optics problem using the lensmaker's equation, 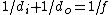 , relating the distances of the object, image, and the focus. , relating the distances of the object, image, and the focus.
Since there are two convex lenses, one can treat the set-up as a telescope. The lens closest to the laser is the objective (with focus 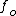 ) and the one closest to the bigger-radius well-collimated beam is the eyepiece ) and the one closest to the bigger-radius well-collimated beam is the eyepiece  . .
The laser-light comes in from 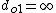 , and thus one has , and thus one has 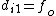 , i.e., the image forms at the focal point. , i.e., the image forms at the focal point.
Using the telescope equation, one has 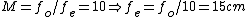 , since one wants a final magnification of 10 (to wit: input beam is 1mm, output beam is 10mm). This narrows down the choices to just (D) and (E). , since one wants a final magnification of 10 (to wit: input beam is 1mm, output beam is 10mm). This narrows down the choices to just (D) and (E).
Since the distance between lenses for a telescope (with incoming light coming from infinity) is given by 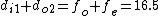 , which relates the distance of the image from the first lens to the distance of the object from the second lens, one arrives at choice (E). (Correction due to user tachyon.) , which relates the distance of the image from the first lens to the distance of the object from the second lens, one arrives at choice (E). (Correction due to user tachyon.)
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Rift
2011-03-22 20:10:40 | this is a beam expander. the objective and eyepiece lenses' placements are reversed. rnrnhttp://www.edmundoptics.com/technical-support/lasers/beam-expanders/?&viewall
Setareh
2011-10-07 09:57:05 |
Yeah, as you said, the placements of objective lens and ocular or eyepiece lens in beam expander are opposite of their placement in telescopes. In telescopes the first lens is objective, while in beam expanders the second one is objective. Thankss!
|
|  | hanin
2009-09-29 21:26:48 | I solved this problem by considering it's like using a telescope reversely:
The beam was enlarged from d=1mm to d=10mm, this means 10x "magnification".
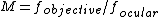
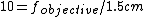
therefore we find the second lens ("objective") has f=15cm. The two lenses should be positioned so that both foci located at the same position, hence the distance = 1.5+15 = 16.5cm
apr2010
2010-04-06 14:36:58 |
very nice
|
|  | anmuhich
2009-04-01 14:27:47 | Envision the light cone converging at the focal point of the first lens, then crossing through the focal point and expanding again. For one focal point the diameter of the cone of light will zero, then for one more it will be back to its original diameter. For each successive focal length the light cone will increase in diameter by 1mm. So you need 10 focal lengths passed the first focal point to reach a 10mm diameter. This already gives you the right answer. To collimate the light again you need just put the right focal length lense at the diameter of the light you want. |  | BeloitPropagandist
2008-11-07 19:31:59 | There is another way. For a compound lens system 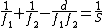 where d is the seperation between lenses. In the case of a collimated beam, S is infinite so the right side goes to zero. Some algebra later and we find that for two thin lenses, if where d is the seperation between lenses. In the case of a collimated beam, S is infinite so the right side goes to zero. Some algebra later and we find that for two thin lenses, if 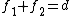 then the beam will always collimate. Some basic geometry and we find that the magnification then the beam will always collimate. Some basic geometry and we find that the magnification 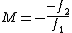
From the first part, the answer is either (c) or (e). For a 10X magnification, the second lens must be 10 times the known lens. Therefore, (E)! |  | Richard
2007-10-08 18:06:12 | Why not just use a little geometry?
You know that the beam from the laser is well collimated, i.e., it emerges parallel. This means it will converge to the focal length of the first lens: 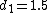 . .
Now if we want to turn this diverging beam again into a collimated beam with width 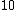 mm, we need another lens with a focal length equal to the distance from the point at which the beam first converged. This configuration creates two similar triangles: mm, we need another lens with a focal length equal to the distance from the point at which the beam first converged. This configuration creates two similar triangles:
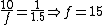
And the distance of the second lens from the first is simply 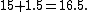
Choice (E) is the answer.
jesford
2008-04-11 13:30:30 |
This is a really nice answer that requires no knowledge of telescopes or lasers!
|
gravity
2010-11-04 13:06:20 |
We did this kind of stuff all the time in our Lasers lab.
You can set the problem up super easy by noting that the triangles on each side of the focal point are similar (since they are both a distance of their respective f away, in order to give a parallel beam).
Or in other words, .5 (half of 1) is to 1.5 as 5 (half of 10) is to 15.
No need to muck about with remembering a bunch of relations - just draw it out and this problem only takes 15 seconds.
|
neo55378008
2012-04-24 19:26:06 |
Excellent solution!
Instead of doing 15+1.5 though, I would just remember the fact that an object placed at the focal point will always converge at infinity, so that rules out D.
|
|  | vroomfondel
2006-11-28 00:58:43 | the answer is here:
http://www.physics.smu.edu/~scalise/emmanual/lens/telescope.gif />
the eyepiece is defined opposite to what yosun has -- semantics error, that\'s all. |  | yosun
2005-11-09 14:34:47 | tachyon: I've defined the eyepiece as the one closest to the magnified beam, so I believe my formula for M is correct.. However, 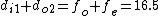 , as you said. I've fixed this in the solutions. Thanks for the correction. , as you said. I've fixed this in the solutions. Thanks for the correction.
yubs
2006-11-01 00:13:16 |
I agree with Tachyon, something is not right here...
If you are saying 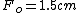 (as given in the question), and we want (as given in the question), and we want 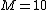 then how can then how can 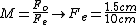 possibly equal 15cm. You're dividing 1.5cm by 10! It has to get smaller! possibly equal 15cm. You're dividing 1.5cm by 10! It has to get smaller!
Like Tachyon said, intuitively we know that if M = 10, the numerator has to be bigger than the denominator.
|
|  | tachyon
2005-11-09 10:38:25 | The way you defined your lenses, the magnification should be M=Fe/Fo. You know the Fe>Fo to allow distance for the laser to get larger. Also, the distance between the two lenses has to be di1+do2=Fe+Fo=16.5. The correct answer is E. |  | tachyon
2005-11-09 10:30:01 | |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
