|
GR9677 #28
|
|
|
Problem
|
|
|
This problem is still being typed. |
Lab Methods }Oscilloscope }Oscilloscope
A superposition of two oscillations has the form  \sin(\frac{\omega_1+\omega_2}{2}) ) . This implies that the cosine term is the amplitude of the combined wave. . This implies that the cosine term is the amplitude of the combined wave.
Similarly, one can see one the lower frequency as the contribution towards the bigger envelope-like wave and the higher-frequency as the zig-zag-gish motion along the envelope.
One oscillation must have a high frequency and the other has a relatively lower frequency. Only choices (D), (A), and (B) show this trait. The high frequency oscillation should have a smaller amplitude than the lower frequency oscillation. Only choices (A) and (D) show this trait. Finally, the amplitude of the lower frequency wave forms the envelope, and the amplitude from that is only about 1 cm; on a 2V scale, this is about 2V---which is closest to choice (D).
|
|
|
Alternate Solutions |
len x 1624
2012-04-16 20:10:16 | Simple Solution:rnrnCount the number of times the small wave occurs within the large wave. For every one large wave there exist six small waves; therefore the frequency of the small wave is 6x the frequency of the large wave. The only instance where the smaller wave has a frequency 6x larger is in choice (D). rnrnChoice (B) is incorrect because the larger wave (3 Volts) has the higher frequency. |  |
|
|
Comments |
lukenlow
2018-06-22 12:27:08 | Excellent info, it is very useful to learn such things in trivial discussions 192.168.O.1 |  | hooverbm
2012-11-01 12:24:49 | A quick way I did this is similar to chemicalsoul's solution.
The wavelength is easy to pick off from the graph, 1cm. We're given the velocity.
v = wavelength*frequency.
f = 500 Hz
This is a beat frequency, thus the difference in frequency between the two oscillations must be very close to 500 Hz.
Choice D is the only solution that satisfies that condition. |  | len x 1624
2012-04-16 20:10:16 | Simple Solution:rnrnCount the number of times the small wave occurs within the large wave. For every one large wave there exist six small waves; therefore the frequency of the small wave is 6x the frequency of the large wave. The only instance where the smaller wave has a frequency 6x larger is in choice (D). rnrnChoice (B) is incorrect because the larger wave (3 Volts) has the higher frequency.
aprilrussell
2018-05-30 03:45:18 |
A quick way I did this is similar to chemicalsoul\'s solution. https://run2.online/run-3 Thanks
|
|  | cathaychris
2011-10-13 21:26:53 | Since the higher frequency oscillation is easy to pick out, note that one period is about 1 cm at .5 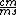 = 2 ms....... = 2 ms....... 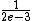 = 500 Hz, which only appears in one place, (D). You can further reassure yourself by noting the high-frequency amplitude is about 1.25 cm, pk-pk * 2 V/cm = 2.5 = 500 Hz, which only appears in one place, (D). You can further reassure yourself by noting the high-frequency amplitude is about 1.25 cm, pk-pk * 2 V/cm = 2.5 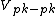 . Remember amplitude is half of the pk-pk value. . Remember amplitude is half of the pk-pk value. |  | mrTrig
2010-10-23 12:42:33 | ****First line typo****
time is missing on left side. should be
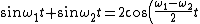}\sin{\left(\frac{\omega_{1}+\omega_{2}}{2}t\right)}) |  | chemicalsoul
2009-10-17 01:50:33 | From the given graph, we can approximate that the wavelength is 1cm and the amplitude is .5 cm=1v. Therefore, the frequency diff between the two waves should be near to 500 Hz and the amp diff should be about 1 v. (D) is the closest ! |  | ravenseldon666
2008-10-25 00:36:44 | the waves are of different amplitudes so how come they add up to the form product of two sines of a frequency sum and frequency difference? |  | dumbguy
2007-10-16 11:05:44 | Don't forget the scales of the oscilliscope. x is equivilant to freq. while y is equivilant to volts. You'll notice that the period of the the higher freq. wave is about 1 cm.( i used the bottoms of the first two) Since it is given that .5cm/ms, you can deduce that 1 cm is 2 ms. T=1/f, so the period is 1000/2 or 500hz. Choice D is the only one that has this. If not coninved, then check the amplitude. The amplitude is a little more then .5cm, which means it has to be a little more then 1 volt, which fits with D and its freq. as well. If you do the same thing for the wave envolope, you will get a freg. less then 100, around 80 and an amplitude of 2.5 volts. Don't forget when drawing the wave envolope to go thru the center of the higher freq. waves. |  | adam
2005-11-09 22:25:22 | From hind sight...
If you count the periods for the high freq that occur during the 1 period of the lower freq you will get a ration about 6:1. This means that 6(low freq)= high freq. This satisfies B and D. But B has the amplitudes wrong (higher freq should have a smaller amplitude than low freq) leaving D as the answer.
flyboy621
2010-10-23 08:02:38 |
This is the way to do it. The smaller wave has 6 times the frequency and half the amplitude of the larger. Choice (D) is the best.
Good ol' hindsight...
|
|  |
|
| Post A Comment! |
You are replying to:
Don't forget the scales of the oscilliscope. x is equivilant to freq. while y is equivilant to volts. You'll notice that the period of the the higher freq. wave is about 1 cm.( i used the bottoms of the first two) Since it is given that .5cm/ms, you can deduce that 1 cm is 2 ms. T=1/f, so the period is 1000/2 or 500hz. Choice D is the only one that has this. If not coninved, then check the amplitude. The amplitude is a little more then .5cm, which means it has to be a little more then 1 volt, which fits with D and its freq. as well. If you do the same thing for the wave envolope, you will get a freg. less then 100, around 80 and an amplitude of 2.5 volts. Don't forget when drawing the wave envolope to go thru the center of the higher freq. waves.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
