|
GR8677 #75
|
|
|
|
|
Alternate Solutions |
oliTUTilo
2012-11-02 21:48:53 | In case you can't remember Kepler's Law (I couldn't), you can jimmy it starting with the circular motion acceleration law and the force of gravity law to get the relation between period and orbit.
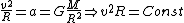 (1) (1)
 (2) (2)
Plugging (2) into (1),
}^2 R=Const\Rightarrow R=T^{\frac{2}{3}}Const)
By the way, for approximating roots (cube roots), I find the surrounding powers (cubes). So
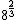 < <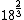 < <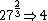 < <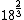 < <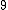 |  | wittensdog
2009-07-26 14:02:16 | In terms of simplifying the radical expression, there's a method I found somewhat useful. If you write out 18 in terms of prime factors, you get 2*3*3. It is then easy to write the square of 18 in terms of prime factors, since you just double the number of each factor, and you have 2*2*3*3*3*3. If you call one of the 3's a 2, which is a somewhat reasonable approximation, then you have 3 3's and 3 2's, resulting in (2*2*2)*(3*3*3). Clearly, taking the cube root of that results in 2*3 = 6. It's not super exact, but certainly close enough to get the right answer. |  |
|
|
Comments |
klestecyca
2018-10-19 04:07:32 | Yosun, I believe after you plug in for k, the 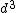 should be in the numerator, not the denominator. should be in the numerator, not the denominator. |  | 62a
2016-09-22 05:34:45 | d is proportional to T^(2/3). So increasing T by a factor of C increases d by a factor of C^(2/3). That\'s probably the easiest and fastest way to proceed. |  | oliTUTilo
2012-11-02 21:48:53 | In case you can't remember Kepler's Law (I couldn't), you can jimmy it starting with the circular motion acceleration law and the force of gravity law to get the relation between period and orbit.
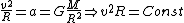 (1) (1)
 (2) (2)
Plugging (2) into (1),
}^2 R=Const\Rightarrow R=T^{\frac{2}{3}}Const)
By the way, for approximating roots (cube roots), I find the surrounding powers (cubes). So
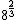 < <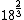 < <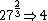 < <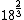 < <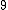
withshirt
2013-11-11 08:00:33 |
your solution is better
|
|  | oliTUTilo
2012-11-02 21:47:09 | In case you can't remember Kepler's Law (I couldn't), you can jimmy it starting with the circular motion acceleration law and the force of gravity law to get the relation between period and orbit.
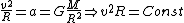 (1) (1)
 (2) (2)
Plugging (2) into (1),
}^2 R=Const\Rightarrow R=T^{\frac{2}{3}}Const)
By the way, for approximating roots (cube roots), I find the surrounding powers (cubes). So
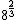 < <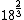 < <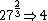 < <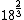 < <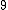 |  | FutureDrSteve
2011-10-27 13:17:18 | Hey all,
I was just looking through my intro physics text, reading about Kepler's Laws and there was a sample problem about geosynchronous orbit. Anyway, if you're a fan of memorization, the radius for geosynchronous orbit is about 4E7m. If you also know the radius of the Earth (abt 6E6m), then this problem just boils down to "how many solar radii equal the radius for geosynchronous orbit?" and you don't need to do any real physics. Of course, you have to know those two values, but now you do! :) |  | neon37
2010-11-03 23:30:02 | One easy thing to do when doing this kind of problem is grouping the prime factors in groups of n if you need to take nth root and factoring those things out then it becomes a lot easier. For example for this problem at one point you should get ![\sqrt[3]{3*3*6*6}](/cgi-bin/mimetex.cgi?\sqrt[3]{3*3*6*6}) so to simplify this, you can do so to simplify this, you can do ![\sqrt[3]{3^3*2*6}](/cgi-bin/mimetex.cgi?\sqrt[3]{3^3*2*6}) which gives which gives ![3\sqrt[3]{12}](/cgi-bin/mimetex.cgi?3\sqrt[3]{12}) and you should know that and you should know that ![\sqrt[3]{12}](/cgi-bin/mimetex.cgi?\sqrt[3]{12}) is more that 2 and less than 3 and closer to 2 than 3. So its obvious that the answer becomes 7. is more that 2 and less than 3 and closer to 2 than 3. So its obvious that the answer becomes 7. |  | wittensdog
2009-07-26 14:02:16 | In terms of simplifying the radical expression, there's a method I found somewhat useful. If you write out 18 in terms of prime factors, you get 2*3*3. It is then easy to write the square of 18 in terms of prime factors, since you just double the number of each factor, and you have 2*2*3*3*3*3. If you call one of the 3's a 2, which is a somewhat reasonable approximation, then you have 3 3's and 3 2's, resulting in (2*2*2)*(3*3*3). Clearly, taking the cube root of that results in 2*3 = 6. It's not super exact, but certainly close enough to get the right answer.
wittensdog
2009-10-07 17:55:00 |
To convince yourself that you shouldn't be worried about the error, even without going and finding the exact values to compare, notice that you're introducing an error on the order of (3/2) ^ 1/3, by flipping a 3 to a 2 underneath the radical.
Now, just by looking at the expression,
(1.5) ^ (1/3)
or the cube root of 1.5, you can tell that it's certainly more than one and less than 1.5, probably closer to the one side (the actual result is something around 1.145, but pretend you don't know that). Now, for sure, this at least tells us we're not introducing anything like a factor of two in error, and looking at the answer choices and how much they're spaced out, we know it's definitely not 3 or 18, since going from a value of 6 to one of those would mean at least a factor of two of error. So you can definitely feel safe about 7.
I know when I type it all out it seems sort of long, but I think being able to approximate like this, and also being aware of how good your approximation is, is something that would be good to be able to do quickly without thinking too much. I mean seriously, how else are you going to calculate something like 18^(2/3) ?? Anyone who thinks they're going to approach it by doing out 18^2 to find 324, and then trying to take the cube root of that, is not going to get far on the test. Even ball-parking it as 400 and trying to take the cube root isn't exactly a walk in the park.
|
insertphyspun
2011-02-19 14:19:47 |
Come on, physicists don't use prime factorization. Ball parking is easy. 18 is 20, 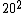 =400. Among the answers, what cubed is about 400? =400. Among the answers, what cubed is about 400? 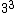 =27, nope. We just did =27, nope. We just did 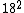 , so clearly the answer is not 18. So it's 7. , so clearly the answer is not 18. So it's 7.
Just to make sure, 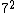 is 50 so is 50 so 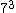 is 350. Close enough. is 350. Close enough.
|
jmkelly
2012-10-03 10:28:47 |
Nice.
|
|  | herrphysik
2006-10-30 00:32:29 | No need to solve for a proportionality factor, just use the form ^2=(s_1/s_2)^3) . Same thing. Also, the exact result I get is . Same thing. Also, the exact result I get is 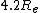 , so I suppose it would actually be , so I suppose it would actually be 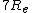 and not and not 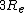 due to the gravitational force being less at the higher orbit? due to the gravitational force being less at the higher orbit?
tin2019
2007-10-29 10:52:42 |
The exact result is 6.868
|
deneb
2018-10-10 05:14:29 |
Agreed, just a simple ratio problem. \r\n\r\nT1 = 4/3 hours\r\nT2 = 24 hours\r\n\r\nR1 = 1 Re\r\nR2 = a * Re\r\n\r\nsolve for a\r\n\r\n18^2 = a^3\r\n\r\na = 18^(2/3)\r\n\r\nwe can approximate 18^(1/3) to be around 2.5, which squared is 6.25. Answer is B.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
