|
GR8677 #74
|
|
|
|
|
Comments |
casseverhart13
2019-09-10 06:12:15 | I enjoyed to find this problem. I like your point of view about this. kitchen remodeling Raleigh |  | whereami
2018-04-09 02:12:01 | what does it mean by \"continuously rotated through 180\" ? |  | Wattson
2015-10-14 09:27:42 | If you forget the equation for intensity transmitted through a polarizer, Sakurai\'s quantum book (chapter one) gives a useful analogy with the Stern-Gerlach experiment, for those who happened to use it.\r\n\r\nJust remember that in sequential S-G setups exactly half of the particles will pass through the first \"filter\" and half of the resulting \"polarized\" beam will pass through each subsequent filter oriented at 45 degrees.\r\n\r\nOf course, knowing that the filters in this problem are also oriented at 45 degrees comes from the symmetry argument evanb gave. |  | neon37
2010-11-03 12:47:58 | Well, it does help to have know about the configuration of polarizers from before. Once you know that when you insert the third one the transmitted is not zero, then you can eliminate A. Then unpolarized light through a polarizer give half intensity. When you pass through the more, the intensity is max only if the polarizers are aligned according to the first. But, it was originally oriented so that no light passes through. This should get rid of C, D and E so remainder is B. |  | thebigshow500
2008-10-13 23:51:00 | There is no need of the trigonometric identity when doing real GRE on this question.
"The polarizers are oriented so that no light emerges through the 2nd polarizer..." - this tells you that the first two polarizers form an 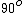 angle. angle.
When the 3rd one is inserted between the first two, it is free to rotate through 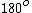 . The maxium fraction of power, 1/8, occurs only when the light is transmitted at . The maxium fraction of power, 1/8, occurs only when the light is transmitted at 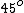 relative to the 1st and 2nd polarizers. relative to the 1st and 2nd polarizers.
cos^2(\theta_2)=\frac{I_o}{2}cos^2(45)cos^2(45)=\frac{I_o}{8}.)
The rest of the angle combinations (e.g. 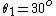 , , 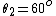 relative to 1st and 2nd polarizers) will give you an even lower power. relative to 1st and 2nd polarizers) will give you an even lower power.
Sometimes, reading questions carefully is a key for a better GRE score! |  | evanb
2008-06-20 15:54:02 | Symmetry dictates that either the min or the max. electric field will be transmitted at 45 degrees. Then, go from there.
wittensdog
2009-10-07 17:14:33 |
When I first started studying physics, I didn't understand why everyone made such a big deal out of symmetry. Now, having studied physics for long enough, I appreciate all of the amazing things it can do.
Assuming that there is some angle which corresponds to maximum light transmission (which we know there must be since from experience with rotating a third polarizer in between two crossed ones we know there are times when there is no light transmission and times when there is some), then considering the symmetry of this setup, it couldn't possibly be anything other than straight down the middle. There would be no reason for it to be on either side of the line that splits the difference between the original two polarizing axes. Then you can go ahead and apply the formulas for light going through a polarizer with some angle (making sure you notice that the original light in UNpolarized!).
|
|  | blah22
2008-04-05 22:33:12 | It is easy to reach the answer via process of elimination here:
After going through the first polarizer, intensity is already cut down to 1/2, this eliminates D and E.
It still has to go through 2 more polarizers which are not parallel to the first, so this eliminates C.
A might be tempting but even general knowledge of how polarization works tells you that you can get some light through two orthogonal polarizers by placing a third in the middle.
Thus, B is left.
jw111
2008-09-01 01:35:34 |
This is a brilliant way posted by blah22.rnrnLet me explain it in detail.rnNOTATION : (pP1:field direction parallel to polarizer 1, dP1: perpendicular to polarizer 1)rnrnAfter pass the P1, only half of energy passed.rnThus  , and the light are all in pP1 state.rnrnYou think they are all in pP1, but that is not true. Actually, half of them are in pP2 and half of them in dP2(suppose P2 is , and the light are all in pP1 state.rnrnYou think they are all in pP1, but that is not true. Actually, half of them are in pP2 and half of them in dP2(suppose P2 is 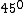 respect to P1, explain letter) when the light comes to the front of P2. rnrnWhen the light passing through P2, the remain field strength is respect to P1, explain letter) when the light comes to the front of P2. rnrnWhen the light passing through P2, the remain field strength is  of before.rnrnP.S.(decomposing vector into of before.rnrnP.S.(decomposing vector into and 45^0(dP2)) ). rnrnSo the power is half again. And all the light is in pP2 state, after passing through P2.rnrnYou think they are all in pP2, but that is not true. Actually, half of them are in pP3 and half of them in dP3 when the light comes to the front of P3.rnrnWhen the light passing through P3, the remain field strength is ). rnrnSo the power is half again. And all the light is in pP2 state, after passing through P2.rnrnYou think they are all in pP2, but that is not true. Actually, half of them are in pP3 and half of them in dP3 when the light comes to the front of P3.rnrnWhen the light passing through P3, the remain field strength is  of before. So the power is half again. And all the light is in pP3 state.rnrnSo the final power is of before. So the power is half again. And all the light is in pP3 state.rnrnSo the final power is 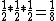 rnrnWHY rnrnWHY 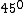 rnrnIf the angle is smaller (to P1), more light passing through P2 you get, but less light pass through P3.rnIf the angle is larger (to P1), less light passing through P2 you get, although more light passing through P3.rnThus, the maximum must happens between them, the rnrnIf the angle is smaller (to P1), more light passing through P2 you get, but less light pass through P3.rnIf the angle is larger (to P1), less light passing through P2 you get, although more light passing through P3.rnThus, the maximum must happens between them, the 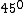 .rn .rn
|
|  | nitin
2006-11-16 13:04:56 | Corrections:
1)cos^2(\theta)=\frac{I}{8}sin^2(2\theta)) . .
2)cos(2\theta)=\frac{I}{4}sin(4\theta)=0) , and , and 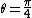 is the value of the angle giving the maximum transmitted power fraction (no need to check for maximality, since is the value of the angle giving the maximum transmitted power fraction (no need to check for maximality, since 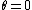 is the only other possible value, but this gives zero transmission, which makes sense since this means polarisers 2 & 3 have the same polarisation directions). is the only other possible value, but this gives zero transmission, which makes sense since this means polarisers 2 & 3 have the same polarisation directions).
spacemanERAU
2009-10-18 19:58:13 |
thank you nitin...i was sitting here wondering how he got sin(Pi/2)=2
so i was gonna rework the problem to see where the mistake was...but then i saw your post...good job
|
ali8
2011-06-29 13:07:22 |
That's excellent, thank :)
|
withshirt
2013-11-11 06:14:07 |
I agree with you. ყოჩაღ!
|
|  | Andresito
2006-03-19 10:02:37 | Yosun, when you use the trigonometric identity, Sin(2*theta) you need to square it and multiply by Intensity/2. The correct expression must then be
Intensity3 = (Intensity/8) * Sine(2*theta).
No need to take a derivative to find the maximum here since Intensity3 has a maximum when the Sine function has a maximum (the argument is pi/2).
That is how you obtain the Intensity/8 result.
Thanks Yosun. |  | agge
2006-03-10 13:52:43 | 1) the angle phi refers to the 2nd polarizer not the 1st
2) plugging in theta=pi/4 to sin(2*theta) gives 1, hence the result would be I/4....
so your reasoning confuses me.. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
