|
GR9677 #88
|
|
|
|
|
Alternate Solutions |
evanb
2008-07-02 13:59:18 | At r = 0, the field must be zero, because an infinitely-small amperian loop contains no current.
At r=c, the field must be zero, because the inner current and the outer current cancel out.
The only graph that satisfies these two contraints is B. |  |
|
|
Comments |
plapas
2009-04-01 13:23:22 | For the coaxial cable one should remember by heart that the field near the axis increases linearly and that the field outside the cable is zero (providing that equal and opposite currents run along the two parts of it). Given this, one can effortlessly to choice (B). |  | ssp
2008-09-07 18:13:00 | I used the condition they give us s << l... If that is true (c), (d) and (e) could approach infinity, so they are out. The in 2 in (a) seems very unphysical to be honest because we are only talking about the portion of a trajectory... So I picked (B) |  | evanb
2008-07-02 13:59:18 | At r = 0, the field must be zero, because an infinitely-small amperian loop contains no current.
At r=c, the field must be zero, because the inner current and the outer current cancel out.
The only graph that satisfies these two contraints is B.
jmason86
2009-10-04 15:21:48 |
Can I get a Hell YeaAH!
Nice solution.
|
dogsandfrogs
2009-10-08 15:18:42 |
Simple and fantastic solution, definitely useful given the time constraint.
|
|  | sawtooth
2007-10-30 02:24:29 | For first stage, apply Ampere's law in a circle with radius 0Reply to this comment |  | newton
2007-09-27 21:58:17 | Amperes law,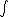 B.dl= B.dl=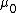 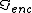
For r=C, 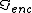 = =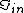 - -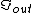 =I-I=0 =I-I=0 |  | welshmj
2007-08-02 20:44:49 | I think the part where you are finding the magnetic field between a and b is actually the magnetic field where r < a not the magnetic field where a
newton
2007-09-27 22:13:05 |
Yes i too think so.The magnetic field linearly increases in the region 0 to a.
In the region between a and b it is linearly decreasing, B=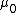 I/2 I/2 r r
|
vsravani
2008-11-04 19:55:07 |
Yes, the linearly increasing field is between 0 to r and not between a-b. The error needs to be corrected.
FYI,
Between a and b, B is of the form
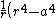)
|
|  | yosun
2005-11-16 23:51:57 | astro_allison: subscripts 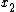 and superscripts and superscripts 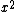 both work. however, the both work. however, the  is due to a file-conversion error; it happens whenever a subscript or superscript ends with the letter n, as in _{n} or ^{n}. and, it's only a file-conversion error... user comment posts should not produce the error if you enter in your equation right. is due to a file-conversion error; it happens whenever a subscript or superscript ends with the letter n, as in _{n} or ^{n}. and, it's only a file-conversion error... user comment posts should not produce the error if you enter in your equation right.
please post a typo-alert (in the comments section of the solution) if you find other solutions with mal-formed equations. |  | astro_allison
2005-11-16 23:13:17 | see, i can't even get it to work! |  | astro_allison
2005-11-16 23:13:03 | I think your subscripts aren't working for I 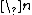 this is in several problems. fyi this is in several problems. fyi
candywr
2023-07-11 18:37:08 |
I tried subscripts on the website I built which is wordleunlimited.co and they are working perfectly fine.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
