|
GR9677 #7
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Elastic Collisions }Elastic Collisions
One determines the velocity of impact of the ball from conservation of energy,
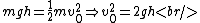
Conservation of momentum gives,
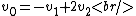
Conservation of kinetic energy gives,
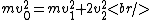
Plug in the momentum and kinetic energy conservation equations to solve for 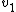 and and 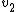 in terms of in terms of 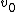 to get to get
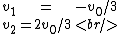
Write yet another conservation of energy equation for the final energy,
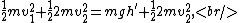
where the condition that the mass 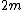 slides on a frictionless plane is used. slides on a frictionless plane is used.
Thus, 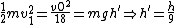 , where the previous result , where the previous result 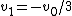 and and 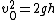 is used. is used.
|
|
|
Alternate Solutions |
amber
2014-10-20 08:36:52 | In CM frame the velocity of the CM before collision is:
V = (m1v1+m2v2) / (m1+m2)
V = mv1i / (3m) = v1i/3
Find v1i by conservation of energy:
0.5 m v1i^2 = mgh ->> v1i = sqrt(2gh)
Plug in to V
V = sqrt(2gh)/3
In CM frame for elastic collisions vi = vf therefore:
KE1f = 0.5 m V^2 = mgh/9
Setting KEif equal to mgh'
mgh/9 = mgh'
h' = h/9
|  | djh101
2014-09-22 15:28:39 | For an elastic collision with one body initially at rest, you can combine the two conservation equations to get:
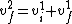
A good formula to remember for the test. Plugging this into the momentum equation then gives 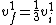 which gives you a height of 1/9 the initial height. which gives you a height of 1/9 the initial height.
In a problem where neither mass is at rest, you can move to a frame where one mass is at rest and then use the above formula to solve for the two final velocities. Of course, if you're switching frames, a COM frame might actually be faster. |  | justin_l
2013-10-17 23:05:32 | Probably the fast way to do this problem in particular.
In elastic collision problems with rational masses,  is always changed by a rational factor. is always changed by a rational factor.
The height it will rise depends on its kinetic energy, 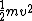 , due to conservation of energy. , due to conservation of energy.
Only one of the answered has a factor that is the square of a rational number -- A: 
owenyang75
2014-10-20 06:28:51 |
Sometimes a vague memory can also be helpful. Take this one for instance,rnit might be a little hard to really remember the exact form of the equations for collision, but you can easily notice that there is something over 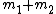 , which is reasonable because problems like this one could be viewed in a CM frame, and then you get the 9 in the answer. , which is reasonable because problems like this one could be viewed in a CM frame, and then you get the 9 in the answer.
|
|  | zuts
2013-09-18 08:29:26 | all of your solutions are so lengthy.
remember
elastic collision momentum and energy are conserved.
inelastic collision just momentum.
so whenever you see a collision just solve with momentum P = m * v don't even worry about elastic or inelastic you hear collision or any word like collision momentum = conserved.
P1=P2
for this problem the first mass is P1=m*v plug into E to find height
1/2 m v^2 + mgh1 = 0
P1^2/2m +mgh1 = 0
solve for P1 you get -P1^2=2mgh1
do the same for P2 but this time the mass is 3m because they stick together.
P2=3mv
3/2 m v^2 + 3mgh2 = 0
3P2^2/18m + 3mgh2 = 0
-P2^2 = 18mgh2
-P1^2=-P2^2
2mgh1 = 18mgh2
h2=2/18 h1 = h1/9
|  | nbwell
2007-10-31 12:08:48 | There is an easier way using conservation of momentum and energy. Consider the ratio of the masses m1 (the ball) and m2 (the brick). The initial momentum into the system is going to be m1 times the initial velocity of m1. After the collision, the momentum is divided between the masses so that the momentum (magnitude) of m1 is half the momentum (magnitude) of m2; put another way, the post collision momentum (magnitude) of m1 is 1/3 of the total initial momentum. Thus we've conserved momentum.
Now to determine the height consider conservation of energy. Momentum is proportional to velocity, and kinetic energy is proportional to velocity squared. Since post collision m1 has 1/3 its initial momentum, it only has 1/9 its initial kinetic energy. As it flies upwards, the kinetic energy is converted to potential energy (mgh). So with only 1/9 the kinetic energy, it can only achieve 1/9 the potential energy and thus only rise to 1/9 its initial height. (you could also have realized this since kinetic energy is proportional to momentum squared)
In short, inspect the ratio of masses to determine how the momentum is going to be divided. Deduce how the reduced momentum will reduce your kinetic energy. Finally realize that this reduction in kinetic energy will equal the reduction in potential energy and the reduction in height. |  |
|
|
Comments |
amber
2014-10-20 08:36:52 | In CM frame the velocity of the CM before collision is:
V = (m1v1+m2v2) / (m1+m2)
V = mv1i / (3m) = v1i/3
Find v1i by conservation of energy:
0.5 m v1i^2 = mgh ->> v1i = sqrt(2gh)
Plug in to V
V = sqrt(2gh)/3
In CM frame for elastic collisions vi = vf therefore:
KE1f = 0.5 m V^2 = mgh/9
Setting KEif equal to mgh'
mgh/9 = mgh'
h' = h/9
|  | djh101
2014-09-22 15:28:39 | For an elastic collision with one body initially at rest, you can combine the two conservation equations to get:
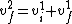
A good formula to remember for the test. Plugging this into the momentum equation then gives 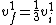 which gives you a height of 1/9 the initial height. which gives you a height of 1/9 the initial height.
In a problem where neither mass is at rest, you can move to a frame where one mass is at rest and then use the above formula to solve for the two final velocities. Of course, if you're switching frames, a COM frame might actually be faster.
djh101
2014-09-22 15:29:51 |
Oops. The subscripts and superscripts should be switched. Well, just note that the 1 and 2 represent the body, not powers.
|
|  | justin_l
2013-10-17 23:05:32 | Probably the fast way to do this problem in particular.
In elastic collision problems with rational masses,  is always changed by a rational factor. is always changed by a rational factor.
The height it will rise depends on its kinetic energy, 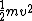 , due to conservation of energy. , due to conservation of energy.
Only one of the answered has a factor that is the square of a rational number -- A: 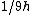
owenyang75
2014-10-20 06:04:15 |
Sometimes a vague memory can also be helpful. Take this one for instance,
it might be a little hard to really remember the exact form of the equations for collision, but you can easily notice that there is something over 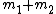 , which is reasonable because problems like this one could be viewed in a CM frame, and then you get the 9 in the answer. , which is reasonable because problems like this one could be viewed in a CM frame, and then you get the 9 in the answer.
|
owenyang75
2014-10-20 06:28:51 |
Sometimes a vague memory can also be helpful. Take this one for instance,rnit might be a little hard to really remember the exact form of the equations for collision, but you can easily notice that there is something over 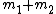 , which is reasonable because problems like this one could be viewed in a CM frame, and then you get the 9 in the answer. , which is reasonable because problems like this one could be viewed in a CM frame, and then you get the 9 in the answer.
|
|  | justin_l
2013-10-17 23:03:42 | Probably the fast way to do this problem in particular.
In elastic collision problems with rational masses, v is always changed by a rational factor.
The height it will rise depends on its kinetic energy, 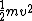
Only one of the answered has a factor that is the square of a rational number -- A: 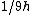 |  | zuts
2013-09-18 08:29:26 | all of your solutions are so lengthy.
remember
elastic collision momentum and energy are conserved.
inelastic collision just momentum.
so whenever you see a collision just solve with momentum P = m * v don't even worry about elastic or inelastic you hear collision or any word like collision momentum = conserved.
P1=P2
for this problem the first mass is P1=m*v plug into E to find height
1/2 m v^2 + mgh1 = 0
P1^2/2m +mgh1 = 0
solve for P1 you get -P1^2=2mgh1
do the same for P2 but this time the mass is 3m because they stick together.
P2=3mv
3/2 m v^2 + 3mgh2 = 0
3P2^2/18m + 3mgh2 = 0
-P2^2 = 18mgh2
-P1^2=-P2^2
2mgh1 = 18mgh2
h2=2/18 h1 = h1/9
postal1248
2013-10-17 18:28:17 |
You got lucky. The masses don't stick together. The mass after collision is not 3m.
|
|  | Kabuto Yakushi
2010-09-05 09:14:40 | It probably would be a good idea to memorize the velocity formulas for elastic collisions:

and
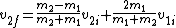
once you get the pattern down the formulas aren't as difficult as they look.
Steve
2011-08-24 14:04:01 |
I derived this same result last night and then explored for equivalent alternate-forms that might be easier to memorize. You might find this easier to remember:
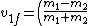v_{1i} + \left(\frac{m_1-m_2}{m_1+m_2}-1\right)v_{2i})
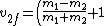v_{1i} + \left(\frac{m_1-m_2}{m_1+m_2}+2\right)v_{2i})
|
|  | sullx
2009-11-04 16:55:07 | Totally irrelavent, but suprisingly you aren't punished for mistaking the problem for an illeastic one if you do it correctly.
If you consider an inelastic collision between the ball and the block, a final mass of 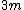 would rise to a height of would rise to a height of 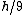 also. also.
|  | shafatmubin
2009-10-29 12:11:08 | There seems to be a slew of collision problems in GRE, relativistic and non-relativistic. So here is a set of collision formulae for a particular case:
Case:
A moving body collides elastically with a stationary body.
m2 = m1[ {p(1,f) -p(1,i)} / {p(1,f) + p(1,i)} ]
(p can be replaced with mv to get:
m2 = m1[ {v(1,f) -v(1,i)} / {v(1,f) + v(1,i)} ]
v(1,f) = v(1,i) * (m1 -m2)/(m1+m2)
v(2,f) = v(1,i) * (2m1)/(m1+m2)
|  | jw111
2008-11-07 09:46:01 | Or you can see it in CM fram
the Vcm = 1/3 to right, so in CM frame
before collision, the velocities are
2/3-> <-1/3
with equal but opposite P, thus after collision
<-2/3 1/3->
return to LAB frame
<-1/3 2/3->
thus u = 1/3v H=1/9h
AER
2009-03-31 13:49:31 |
I think this is definitely the fastest and easiest way to do the problem.
|
wittensdog
2009-10-15 16:38:51 |
Agreed, this was by far the fastest method I found. It spares one from having to memorize the formula for what happens when a moving body hits a still one.
And if you realize how to find the CM frame in general, it'll save you if they throw you a problem where both particles are originally moving at each other with whatever speeds. Essentially, if you have particles with masses A and B and velocities v and w, to find the velocity f of the CM frame, you have,
A(v - f) + B(w - f) = 0
Which is easily solvable for f. You then subtract f from the velocities, flip their signs, since in this frame they rebound, and then add f back to the velocities.
You don't even ever have to find out what the speed of the smaller mass is in this problem when it hits. You can just find that it's -1/3 of what it was originally, telling you it should go back up to 1/9 of its height.
|
|  | jw111
2008-11-04 22:54:11 | *******may not be helpful********
set m=1, v=1, g=1, (then h is in new unit) h is
(1/2)*1*1*1 = 1*1*h
suppose the new velocities are u for m, and u' for 2m
with conservation laws, we have
1 = -u +2u' .................(1)
1 = uu+ 2u'u'...............(2)
we don't have to find out u and u', since the new height, H, is found by
(1/2)*1*u*u = h*u*u = H
you may put choices into (1) and (2), and find out (A) is correct, OR
together with the choices,
u -> rational(A) or irrational(B-E)
if u is irrational
1 = irra + irra .............(1)
1 = ra + irra(in this case) .............(2) NOT HOLD
thus, choose (A)
jw111
2008-11-04 23:03:11 |
for example,
H=uuh, for choice, (A), u = 1/3.
|
|  | nbwell
2007-10-31 12:08:48 | There is an easier way using conservation of momentum and energy. Consider the ratio of the masses m1 (the ball) and m2 (the brick). The initial momentum into the system is going to be m1 times the initial velocity of m1. After the collision, the momentum is divided between the masses so that the momentum (magnitude) of m1 is half the momentum (magnitude) of m2; put another way, the post collision momentum (magnitude) of m1 is 1/3 of the total initial momentum. Thus we've conserved momentum.
Now to determine the height consider conservation of energy. Momentum is proportional to velocity, and kinetic energy is proportional to velocity squared. Since post collision m1 has 1/3 its initial momentum, it only has 1/9 its initial kinetic energy. As it flies upwards, the kinetic energy is converted to potential energy (mgh). So with only 1/9 the kinetic energy, it can only achieve 1/9 the potential energy and thus only rise to 1/9 its initial height. (you could also have realized this since kinetic energy is proportional to momentum squared)
In short, inspect the ratio of masses to determine how the momentum is going to be divided. Deduce how the reduced momentum will reduce your kinetic energy. Finally realize that this reduction in kinetic energy will equal the reduction in potential energy and the reduction in height.
blah22
2008-02-14 09:48:43 |
I disagree with this method. I think your reasoning only works for the specific case of mass ratio of 1:2.
If the ratio were 1:3, by your reasoning after the collision m1 should have 1/3 of m2's momentum so m1 will have 1/4 of the total initial momentum, correct? Then you would square this number and the final height would only be 1/16 of its initial height. But if you run the correct formula that Richard posted below, you see that after such a collision m1's velocity is half of its initial velocity after collision, squaring THAT you get a final height of 1/4 initial height.
The latter solution seems more plausible to me, as you increase the relative mass of m2, m1 should gain more height...not less. Going from 1/9 -> 1/4 rather than 1/9 -> 1/16 with your reasoning. Because if you toss a ball at the earth it returns with nearly all of its energy.
|
isina
2008-10-16 15:09:02 |
not true, only applies to this specific situation. It requires some mathematical manipulation if you want to get the most general form as given above, but when you plug in the numbers, equations are usually easier to solve...
|
|  | Richard
2007-09-24 23:45:12 | As much as I like all of your solutions, I don't think they are really viable in 1.7 minutes. This is how I think it should be done:
You should recall that when you have a perfectly elastic collision with one mass initially at rest, there is a very succint relation between the velocites, namely,
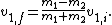

Of course we only need the first one: 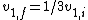 . .
Then, realizing (remembering) that 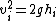 , and using conservation of energy, , and using conservation of energy, 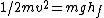 we have, we have,
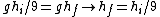
Life is so much easier when you remember the right things.
phys2718
2008-10-03 11:38:24 |
Also note the similarity of the relation between the initial and final velocities to the relation of the transmission and reflection coefficients for waves crossing from one medium to another. I think Richard is right, these expressions are just worth memorizing for a number of different problems.
|
reverbtank
2009-08-18 12:22:19 |
I think this is definitely the best way to do this problem. Everyone on the forum has solved this problem in freshman physics using brute force of E and p conservation. Why bother doing the same thing twice? Memorize these formulas and use your real brain power on something you haven't seen before.
|
|  | cyberdeathreaper
2006-12-31 15:35:53 | The direction of v1 is indeed negative, but its scalar value is not. Therefore, this equation is correct:

but this solution is not:
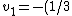v_0)
If it were, then your assumption that v1 moves to the left would be wrong. The correct answer is:
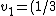v_0)
(See my algebra in the other post to verify how I got this value)
NOTE: The reason the typo doesn't impact the final answer is because v_1 is squared in the final equation, eliminating its sign.
|  | cyberdeathreaper
2006-12-30 16:23:08 | For those interested, here is an expanded explanation of how to get v1 and v2:
First solve for v1 in terms of v0 and v2 from your conservation of momentum equation:

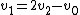
Now solve for v2 in terms of v0 from your conservation of kinetic energy equation, substituting for v1 the equation we just found above:
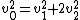
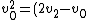^2 + 2v^2_2)
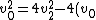(v_2) + v^2_0 + 2v^2_2)
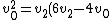 + v^2_0)
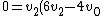)
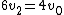
v_0)
Now substitute v2 back into your equation for v1, to get:
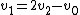
v_0 - v_0)
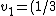v_0)
Thus giving you the answers obtained in the solution provided. |  | senatez
2006-11-01 10:44:16 | Can you explain in greater detail? I can solve it, but I run into some messy algebra with quadratic equations. Can you explain how you so elegantly obtained these values? |  | yubs
2006-10-22 18:25:19 | (Sorry, it won't let me edit my previous post, tells me I should login, but I am logged in...)
I'm a bit confused here and I think there may be a typo.
In the third equation, is a 'm' missing from the third term? Shouldn't it read:

Also, I'm having trouble getting your solution for  & & 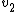 . Could you elaborate on "plug in the equations? . Could you elaborate on "plug in the equations?
many thanks! |  | yubs
2006-10-22 18:10:31 | I'm a bit confused here and I think there may be some typos.
I think there is a 'm' missing from the third equation. Shouldn't it read:
mV_o^2 = mV_1^2 + 2mV_2^2
Also, I'm having trouble getting your solution for V_1 & V_2. Could you elaborate on "plug in the equations?
many thanks! |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
