ETScustomer
2017-09-28 21:04:43 | Here\'s to see why the frequency is not always changing and rule out (E).\r\nWe have the differential equation:\r\n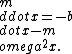 \r\nThat is,\r\n \r\nThat is,\r\n\\left(D-\\frac{-\\frac bm+\\sqrt{\\frac{b^2}{m^2}+4\\omega^2}}2\\right)x.) \r\nThe general solution is\r\n \r\nThe general solution is\r\n \r\nAssuming we\'re not too damped, the new angular frequency is less than the old \r\nAssuming we\'re not too damped, the new angular frequency is less than the old 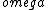 . Thus the period is a constant in time that is larger than . Thus the period is a constant in time that is larger than 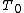 . .
ETScustomer
2017-09-28 21:06:16 |
Woah, that looked nice in the preview, but good luck reading that here.\r\n
|
|  |
GRE1995
2016-09-26 11:09:10 | A physical way to view this problem would be to consider a pendulum displaced from equilibrium by a set distance, and then returning to it. The presence of damping should make the pendulum slower at every point, and hence the answer is (B) or (E). (Notice that for a simple pendulum period independent of damping, so it does not make a difference that the damped pendulum would get to a lower height). Not sure how to rule out E, but you could do it if you recalled the graph |  |
someone
2011-11-05 10:30:19 | If you forgot it, you can quickly derive it
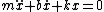 . You know solutions will be of the form . You know solutions will be of the form 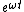 substitute and write down the quadratic substitute and write down the quadratic 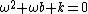
Solutions to this are 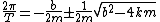
The first term is the exponentially decaying envelop and the second term would be imaginary which causes the oscillations (check that for b=0 it goes to 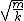 ). So we know that $b^2- 4km <0 \Rightarrow $ frequency is smaller therefore, time period is larger. ). So we know that $b^2- 4km <0 \Rightarrow $ frequency is smaller therefore, time period is larger.
|  |
Steve
2011-08-24 14:36:27 | I missed this problem the first time (put B) because I think I was thinking about 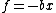 instead of instead of 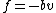 . .
Can anyone confirm that a damping force 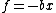 (where x=0 is the equilibrium position of the oscillation) would decrease the period? (where x=0 is the equilibrium position of the oscillation) would decrease the period?
physick
2011-10-09 07:51:22 |
The force you describe is not a damping force, it is a restorative spring force. The form is the same as Hooke's Law, 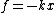 . .
|
|  |
Kabuto Yakushi
2010-09-05 09:39:38 | One can see at once that the answer must be either (B) or (A). We know that when a linearly resistive force is introduced to harmonic oscillations the period: 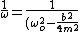^{\frac{1}{2}}}) will not be same as the natural period. Since (B) and (A) cannot both be false it must be one or the other, this takes out (C), (D), and (E). Common sense tells us that the oscillations won't speed up when a resistive force is applied! Therefore the answer is (A). QED. Not very rigorous, but saves time on the GRE. will not be same as the natural period. Since (B) and (A) cannot both be false it must be one or the other, this takes out (C), (D), and (E). Common sense tells us that the oscillations won't speed up when a resistive force is applied! Therefore the answer is (A). QED. Not very rigorous, but saves time on the GRE. |  |
joshfr3
2010-05-27 17:38:16 | For the record, the original answer should be reworded to exclude the part that states "As the amplitude shrinks, the period increases." This would imply that the frequency is constantly changing, which, it is not. The way the answer is worded makes testers believe that (E) could be a potential answer: (E) constantly changing period.
maryami
2011-03-31 04:29:37 |
This is a false comment,period of oscillator is not related to amplitude of oscillations,as T=2pi sqrt(m/k)
|
pam d
2011-09-11 17:32:06 |
Actually joshfr3 is 100% correct here. Maryami misread his comment. Furthermore, the equation maryami supplied only applies to non-damped systems.
|
|  |
Kentai
2009-11-05 22:08:52 | with the equation change from x'' = -w^2 to x'' = -bx' - w^2 x, w must become smaller to compensate the -bx' term, hence the period increase. |  |
jmason86
2009-10-04 13:26:22 | No one has addressed the other options that ETS gives us. I thought that (D) was correct because of limits. If b--> that implies an infinite force acting against the oscillator, which I would imagine would completely destroy the period because it would just stop moving. If b-->0 then you have no damping effect at all and it should behave like an ideal SHO with a period of that implies an infinite force acting against the oscillator, which I would imagine would completely destroy the period because it would just stop moving. If b-->0 then you have no damping effect at all and it should behave like an ideal SHO with a period of 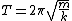 . .
Why is this not correct?!
kroner
2009-10-09 19:27:03 |
The period does increase with increasing b, but it's not a linear relationship. See the formula provided by sharpstones below.
|
|  |
phun_lover
2009-09-29 17:56:23 | This question is somewhat confusing since a damped oscillator doesn't have a well-defined period, in the sense that it's position isn't a periodic function of time. However, it's position can be written as a decaying exponential times a periodic function (if the damping is in the correct range), and so what they want here is the period of that periodic factor--easily solved for from the corresponding differential equation. |  |
cobrachi
2008-10-31 22:14:48 | It's simple to think of this conceptually. The new force is in the opposite direction of the velocity so it will act against the motion of the particle. Thus, it decreases the angular frequency and since T=2pi/w --> a smaller w results in a larger T. |  |
greenfruit
2008-10-31 08:36:12 | Question about the soln: Why can we conclude that as amplitude shrinks period increases? |  |
gn0m0n
2008-10-20 01:22:45 | To echo a couple of questions and hopefully clarify them: do we mean that the period is greater than when it was undamped (ie, but still constant once it is damped) or do we mean it is changing in time once the damping is applied?
gn0m0n
2008-10-20 01:24:19 |
I'd like to ask the same thing about the amplitude.
|
|  |
sharpstones
2007-04-02 19:45:51 | Just to tex it out. The general solution to a damped oscillator is:  where where 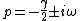 where where 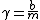 is the damping term and is the damping term and 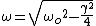 is the frequency of the solution is the frequency of the solution
if omega is real (which is the underdamped case:  ) you will have oscillations which do in fact have a constant period but will have decreasing amplitude from the ) you will have oscillations which do in fact have a constant period but will have decreasing amplitude from the 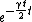 . clearly the frequency . clearly the frequency  will be less then the original frequency will be less then the original frequency 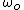 so the period will be greater. so the period will be greater.
sharpstones
2007-04-02 19:46:55 |
that should be 
|
blah22
2008-02-14 11:02:07 |
I'm confused. Why do you say you will have oscillations which have a constant period and in the next sentence say the frequency will clearly be less?
|
gt2009
2009-06-28 13:20:30 |
Both periods are constant, but the damped period is greater than the undamped period.
|
|  |
huanggyellow
2007-03-20 07:28:47 | How about choice (E)? Surely the period is constantly changing (increasing)?
mhas035
2007-03-21 21:42:23 |
The frequency of an underdamped oscillator is omega = omega{undamped}*sqrt(1-b.^2/4mk), i.e. smaller than the undamped frequency, and constant.
|
|  |
