|
GR9677 #54
|
|
|
|
|
Alternate Solutions |
dc771957
2016-10-24 15:04:54 | So what I did was take the real parts of the original wave. You see that x will look like cos and y will look like -cos, as many people have stated. So we know that when x=0, y=0. Then you can see that when x=1, y=-1 and vice versa. Plotting just these three points you see that the answer is B. |  | nerv
2012-11-09 14:15:26 | Note that 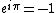 , so , so
![\vec{E} = (E,-E) e^{i[kz-\omega t]}](/cgi-bin/mimetex.cgi?\vec{E} = (E,-E) e^{i[kz-\omega t]}) . .
But ) is just a vector is just a vector 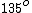 to the x-axis, i.e. (B). to the x-axis, i.e. (B).
|  | flyboy621
2010-10-24 17:36:41 | I think the easiest way is to draw the axes as described in the problem (looking down the z axis toward the origin, and make a sketch of the first quarter-period or so.
Clearly the x component goes like cos(z-t) and the y component goes like -cos(z-t) because of the phase difference of  . If you sketch that, you can quickly see that the two components are always in phase, and the resultant E-field points in the +x, -y direction, or the -x, +y direction. Thus (B) is correct. . If you sketch that, you can quickly see that the two components are always in phase, and the resultant E-field points in the +x, -y direction, or the -x, +y direction. Thus (B) is correct. |  |
|
|
Comments |
dc771957
2016-10-24 15:04:54 | So what I did was take the real parts of the original wave. You see that x will look like cos and y will look like -cos, as many people have stated. So we know that when x=0, y=0. Then you can see that when x=1, y=-1 and vice versa. Plotting just these three points you see that the answer is B. |  | nerv
2012-11-09 14:15:26 | Note that 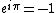 , so , so
![\vec{E} = (E,-E) e^{i[kz-\omega t]}](/cgi-bin/mimetex.cgi?\vec{E} = (E,-E) e^{i[kz-\omega t]}) . .
But ) is just a vector is just a vector 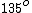 to the x-axis, i.e. (B). to the x-axis, i.e. (B).
|  | mpdude8
2012-04-20 15:35:37 | I just pictures what was going on in my mind. On a piece of paper, you have the combination of something going in the -x direction and the -y direction. The phase shift pi swings the -y direction around to the +y direction. The net wave is a combination of this -- 135 degrees from the x-axis.
The fact that you're viewing from the z-plane just makes the wave look like a line. |  | someone
2011-11-06 16:02:58 | You can do it by retaining the complex exponentials. Let the phase 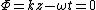 then you have then you have 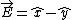 . The polarization is linear, so they must pass thorough the origin together to describe a line of angle . The polarization is linear, so they must pass thorough the origin together to describe a line of angle 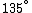 |  | flyboy621
2010-10-24 17:36:41 | I think the easiest way is to draw the axes as described in the problem (looking down the z axis toward the origin, and make a sketch of the first quarter-period or so.
Clearly the x component goes like cos(z-t) and the y component goes like -cos(z-t) because of the phase difference of  . If you sketch that, you can quickly see that the two components are always in phase, and the resultant E-field points in the +x, -y direction, or the -x, +y direction. Thus (B) is correct. . If you sketch that, you can quickly see that the two components are always in phase, and the resultant E-field points in the +x, -y direction, or the -x, +y direction. Thus (B) is correct. |  | georgi
2007-08-30 22:16:29 | there is a really really simple way to do this. note you get a circle iff the phase diff is a multiple of pi/2. note that if phase diff is zero you get a line in the 1st quadrant and thus for pi shift you must get the only other solutions that gives a line which is B the 135 degree line.
dumbguy
2007-10-16 19:22:21 |
For the circle, I'm guessing that what if it is out of phase by -pi/2 it will be counter clockwise and pi/e clockwise? am I correct or is it the other way around?
|
shak
2010-10-23 12:48:07 |
no any solution makes sense for me..may be because i am kinda dubm!:) can anyone clarify...at t=0, E1 is in the x direction , and E2 is in the -y direction , and resultant is in the fourth quarter which is not 135 degree to the +x axis, but -45 degree..
thank you for reply..
|
ngendler
2015-10-23 03:58:18 |
The line at -45 degrees is the same line that goes through 135 degrees (135+180 = 360-45)
|
|  | poong-ryu-do
2005-12-08 21:32:30 | There's a way eaiesr way to do this.
1. see that if waves are in phase a 45 degree straight line is formed y=mx;E1=E2 so x=y; m=1;theta= 45
2. note that wave 1 wave is shifted by pi, hence y=-x;theta =-45or 90+45=135.
gawd havnt got all day to do this! athough its nice to have a proof though.
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
