|
GR9677 #55
|
|
|
|
|
Alternate Solutions |
dc771957
2016-10-24 17:41:17 | Yo fuck latex and whatnot, heres my solution. Intensity a.k.a. irradiance is going to be proportional to the superposition of E1 and E2 dotted with itself. So we will have ) dotted with itself. This will give us dotted with itself. This will give us ) . E1 dot E2 will be zero, since the two waves are orthogonal and polarized perpendicularly to each other. So the final intensity will be proportional to E1^2 + E2^2 . E1 dot E2 will be zero, since the two waves are orthogonal and polarized perpendicularly to each other. So the final intensity will be proportional to E1^2 + E2^2 |  |
|
|
Comments |
Hassan0013
2018-10-12 15:08:27 | I think the better way is to just use the \\\\\r\n\r\n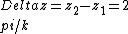 \\\\\r\n\r\nand again combine both 2 waves to make the vector for the electric field.\r\n\r\nnow if we calculate the vector\'s magnitude we easily find the solution for choice (A)\r\n\r\nthis is recombination after portions : \\\\\r\n\r\n \\\\\r\n\r\nand again combine both 2 waves to make the vector for the electric field.\r\n\r\nnow if we calculate the vector\'s magnitude we easily find the solution for choice (A)\r\n\r\nthis is recombination after portions : \\\\\r\n\r\n} + E_2 e^{i(k z_1 + 2\\pi k - \\omega t + \\pi)} ) \\\\\r\n\r\n\r\nnow it needs just to calculate the magnitude of E to get the answer...\r\n \\\\\r\n\r\n\r\nnow it needs just to calculate the magnitude of E to get the answer...\r\n |  | Hassan0013
2018-10-12 15:05:09 | I think the better way is to just use the 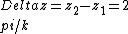 \r\nand again combine both 2 waves to make the vector for the electric field.\r\n\r\nnow if we calculate the vector\'s magnitude we easily find the solution for choice (A)\r\n\r\nthis is recombination after portions : \r\n \r\nand again combine both 2 waves to make the vector for the electric field.\r\n\r\nnow if we calculate the vector\'s magnitude we easily find the solution for choice (A)\r\n\r\nthis is recombination after portions : \r\n} + E_2 e^{i(k z_1 + 2\\pi k - \\omega t + \\pi)} ) \r\n\r\nnow it needs just to calculate the magnitude of E to get the answer...\r\n \r\n\r\nnow it needs just to calculate the magnitude of E to get the answer...\r\n |  | lukenlow
2018-06-22 12:29:34 | An excellent and very simple idea, like all the ingenious in this world, thank you very much for your help 192.168.1.1 |  | dc771957
2016-10-24 17:41:17 | Yo fuck latex and whatnot, heres my solution. Intensity a.k.a. irradiance is going to be proportional to the superposition of E1 and E2 dotted with itself. So we will have ) dotted with itself. This will give us dotted with itself. This will give us ) . E1 dot E2 will be zero, since the two waves are orthogonal and polarized perpendicularly to each other. So the final intensity will be proportional to E1^2 + E2^2 . E1 dot E2 will be zero, since the two waves are orthogonal and polarized perpendicularly to each other. So the final intensity will be proportional to E1^2 + E2^2
dc771957
2016-10-24 17:42:22 |
GODDAMNIT I HATE LATEX. Im so glad im only taking the physics GRE and not trying to learn latex right now
|
|  | giraffe
2014-10-21 01:43:30 | I think the reason why we choose A is E_tot = Sqrt(E1^2*cos^2 + E2^2*cos^2 ), and Intensity equals to E_tot ^2.
While the question asks "the average intensity will be proportional to what", so the answer is the sum of square.
If we calculate the average in a whole period, it would be half of the answer, but still, proportional, so A anyway. |  | pam d
2011-09-17 12:56:47 | Can somebody give me a reason why decoupling the waves makes their intensities add differently? They are already made up of perpendicular polarizations and they have the same optical path length when separated. I honestly would have given same answer if the waves had not been decoupled. Thanks!
hjq1990
2012-10-13 19:06:31 |
Hey man, here optical path difference relates to the X-polarized vector and the Y-polarized one. That is, when we assume that for the X-vector, z=t=0, then for Y-vector we will have z=2*Pi/k, and t=0. These has been expressed by Richard before, just not clearly expressed.
|
maxdp
2013-09-26 10:23:54 |
Pam, I think if they hadn't been decoupled you would calculate it like this:
Ave. Intensity ~ (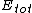 )^2 )^2
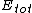 = the vector sum of the two components = the vector sum of the two components
= 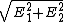
 Ave. Intensity ~ Ave. Intensity ~ 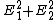
So you get the same answer! Just through different means. I think the reason they were split up in the problem is just to mess with your mind about path length, which I believe should make no difference when it comes to average intensity (but only because they're independent - if two x-components underwent a path length difference and recombined, that could easily affect their total intensity, I believe).
And if you're curious about the constants that are the difference here between "proportional" and "equal to", check out this link:
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/emwv.html
(bottom of page)
|
|  | wikiwert
2010-10-03 09:32:33 | Em...I think I should be more prudent with my comments. I have re-read my wave notes and the definition of intensity is proportional to the time average of E^2. I think this makes sense because the intensity one sees (at least with the naked eye) are constant in time: light frequency >> 25Hz. The time average of a cos^2 or sin^2 is 1/2, but the question says "proportional to". However, in yosunīs solution, I am not sure I = |E1|^2 is correct. Isnīt a 1/2 missing? Although I guess it depends in the proportionality factor you use in the intensity definition. Anyway, as the waves are perpendicular, the path difference does not matter right? It wouldnīt be the first problem with unnecessary information. I hope this comment is useful in some way for someone. |  | wikiwert
2010-09-22 08:15:15 | The solution(s) are not correct. In this case there is no interference becuase the waves are in perpendicular directions, as it has already been mentioned. But in general, one has to consider the total field. Also, the intensity due to x polarized field is not E1^2, but E1^2*cos^2(kz-wt), because E1vector= E1cos(kz-wt) xversor. So the path difference is important because (zo: position of the screen) I = |E|^2= E1^2 cos^2 (kzo - wt) + E2^2 cos^2(kzo-wt+pi+2pi) = E1^2 cos^2 (kzo - wt) + E2^2 sin^2(kz - wt) = E1^2 because E1=E2.
faith
2010-10-17 23:46:19 |
you've made an error. E1^2 cos^2 (kzo - wt) + E2^2 cos^2(kzo-wt+pi+2pi)
should be this instead
E1^2 cos^2 (kzo - wt)-E2^2 cos^2 (kzo - wt).
then you'd eventually get zero, providing E1=E2 still holds.
|
|  | tinytoon
2008-11-03 22:05:31 | If you happen to remember that the intensity is proportional to 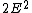 , then the relation falls out. , then the relation falls out.
Because they are decoupled, as Yosun mentioned, they add independently. The first polarization is in the  -direction, the intensity reduces by -direction, the intensity reduces by 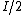 . Therefore you are left with . Therefore you are left with 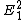
It is same for the 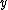 -direction and you just add the two in the end, getting: -direction and you just add the two in the end, getting:
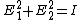 |  | tareq
2007-10-05 05:03:27 | The solution of Yosun Chang is wrong ! When the waves recombine, we have first to calculate the amplitude of the resultant wave to account for any interference effect and use it to calculate the intensity. This is done in the first comment above, by Richard.
sawtooth
2007-10-28 17:45:43 |
No interference for vertical polarisations ! If you insist on taking ^2) , the interference contribution is , the interference contribution is 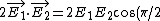 = 0) . .
|
|  | Richard
2007-09-26 17:38:50 | There is a slightly longer, more mathematically rigorous way to get the same answer:
if the optical path difference is 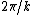 , the field becomes (letting t and z go to zero) , the field becomes (letting t and z go to zero)
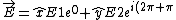}=\hat{x}E1-\hat{y}E2) , taking the real part. , taking the real part.
The intensity is proportional to the magnitude squared of this vector: 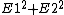 (A) is the answer. (A) is the answer. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
