|
GR9677 #48
|
|
|
|
|
Alternate Solutions |
tdl17
2019-01-03 21:16:15 | Since the particles only took one half-life, which is 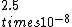 seconds, to travel 15m, it must be traveling close to the speed of light. \\\\r\\\\n\\\\r\\\\nAssume the speed of the particles is some fraction of the speed of light and let this fraction be seconds, to travel 15m, it must be traveling close to the speed of light. \\\\r\\\\n\\\\r\\\\nAssume the speed of the particles is some fraction of the speed of light and let this fraction be  , we now have , we now have  . \\\\r\\\\n\\\\r\\\\nUsing . \\\\r\\\\n\\\\r\\\\nUsing 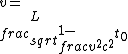 , we can replace v with ac and from there, you can solve for a and that should get you to , we can replace v with ac and from there, you can solve for a and that should get you to 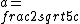 , which is choice C. , which is choice C. |  | Mexicana
2007-10-03 18:06:00 | The second easiest way to solve this, after 'banana's solution' (which is reeeally nice btw!) is just to simply solve for  , getting , getting 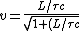^2)}} ) and then just do the ratio and then just do the ratio 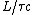 , which is reeally easy to calculate since the lifetime is given in units of , which is reeally easy to calculate since the lifetime is given in units of 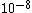 and and 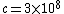 .... Hence, the nice ratio of .... Hence, the nice ratio of 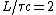 exact. exact. |  |
|
|
Comments |
sunnysunny
2019-08-07 04:40:20 | Your site has a lot of useful information for myself. I visit regularly. Hope to have more quality items.\r\nsubway surfers |  | casseverhart13
2019-06-12 02:24:57 | I adore this weblog, wonderful content for problem solving and I am going to bookmark this website for future updates. click here\r\n |  | casseverhart13
2019-06-12 02:14:10 | I adore this weblog, wonderful content for problem solving and I am going to bookmark this website for future updates. click here\r\n |  | fredluis721
2019-06-10 11:34:08 | Thanks for the information on this. I really enjoy the write up. tile installer |  | tdl17
2019-01-03 21:16:15 | Since the particles only took one half-life, which is 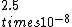 seconds, to travel 15m, it must be traveling close to the speed of light. \\\\r\\\\n\\\\r\\\\nAssume the speed of the particles is some fraction of the speed of light and let this fraction be seconds, to travel 15m, it must be traveling close to the speed of light. \\\\r\\\\n\\\\r\\\\nAssume the speed of the particles is some fraction of the speed of light and let this fraction be  , we now have , we now have  . \\\\r\\\\n\\\\r\\\\nUsing . \\\\r\\\\n\\\\r\\\\nUsing 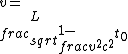 , we can replace v with ac and from there, you can solve for a and that should get you to , we can replace v with ac and from there, you can solve for a and that should get you to 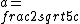 , which is choice C. , which is choice C. |  | psitae
2016-10-27 14:27:54 | probably very close to the speed of light --> 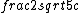 |  | bcomnes
2011-11-02 15:06:43 | I found the solution confusing as written. This is my attempt to make it more clear to myself.rnrnGiven: rnDistance traveled 15m.rnHalf life of Pion is 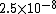 seconds.rnrnWhat we do:rnThe particles move relativistically, hinted at given the subject matter.rnrnSince the pion is moving, its clock runs slower than the lab clock. After traveling 15m, it has decayed less than another pion sample that is not moving, so it appears to have moved faster than the speed of light in order to traverse 15m and only decay 1 half life. The pion only decays for seconds.rnrnWhat we do:rnThe particles move relativistically, hinted at given the subject matter.rnrnSince the pion is moving, its clock runs slower than the lab clock. After traveling 15m, it has decayed less than another pion sample that is not moving, so it appears to have moved faster than the speed of light in order to traverse 15m and only decay 1 half life. The pion only decays for 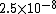 s since only one half of the pions show up. This is our proper time s since only one half of the pions show up. This is our proper time 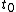 .rnrnDefine the speed of the pion in the lab frame. .rnrnDefine the speed of the pion in the lab frame. 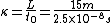 Notice that 15/2.5 = 6 and we get Notice that 15/2.5 = 6 and we get 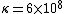 or or 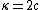 rnrnWe want the speed of the pion that the pion actually feels (or in the pions frame), rnrnWe want the speed of the pion that the pion actually feels (or in the pions frame), 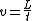 .rnrnRemembering our basic time dilation formula .rnrnRemembering our basic time dilation formula 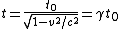 , all we need to do now is solve for v.rnrnPlug in: , all we need to do now is solve for v.rnrnPlug in:  Skipping some algebra Skipping some algebra 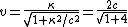 rnrnYou need to remember rnrnYou need to remember 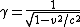 of course, but also you could remember where, of course, but also you could remember where,  is the speed of the particle that the rest frame sees and v is the actual speed of the moving particle as the particle experiences, that is the speed of the particle that the rest frame sees and v is the actual speed of the moving particle as the particle experiences, that 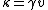 , or conversely define , or conversely define 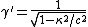 and remember that and remember that 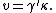
bcomnes
2011-11-02 15:08:31 |
I found the solution confusing as written. This is my attempt to make it more clear to myself.
Given:
Distance traveled 15m.
Half life of Pion is 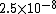 seconds. seconds.
What we do:
The particles move relativistically, hinted at given the subject matter.
Since the pion is moving, its clock runs slower than the lab clock. After traveling 15m, it has decayed less than another pion sample that is not moving, so it appears to have moved faster than the speed of light in order to traverse 15m and only decay 1 half life. The pion only decays for 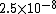 s since only one half of the pions show up. This is our proper time s since only one half of the pions show up. This is our proper time 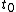 . .
Define the speed of the pion in the lab frame. 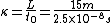 Notice that 15/2.5 = 6 and we get Notice that 15/2.5 = 6 and we get 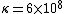 or or 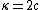
We want the speed of the pion that the pion actually feels (or in the pions frame), 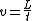 . .
Remembering our basic time dilation formula 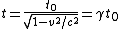 , all we need to do now is solve for v. , all we need to do now is solve for v.
Plug in:  Skipping some algebra Skipping some algebra 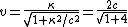
You need to remember 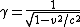 of course, but also you could remember where, of course, but also you could remember where,  is the speed of the particle that the rest frame sees and v is the actual speed of the moving particle as the particle experiences, that is the speed of the particle that the rest frame sees and v is the actual speed of the moving particle as the particle experiences, that 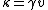 , or conversely define , or conversely define 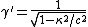 and remember that and remember that 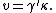
|
bcomnes
2011-11-02 15:09:10 |
Sorry to double post but the first post was totally garbled.
|
|  | CarlBrannen
2010-10-07 14:50:48 | The speeds are in multiples of c so use c=1. We have a messy half life time and a clean distance in the problem so work in meters. To convert the half-life from seconds to meters use 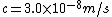 to get 7.5 meters. to get 7.5 meters.
The equation for movement is distance = velocity x time, so we have 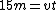 . In the rest frame of the meson the time is 7.5 meters. But time is stretched by the gamma factor so we have: . In the rest frame of the meson the time is 7.5 meters. But time is stretched by the gamma factor so we have:
 then then
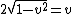 then then
 = v^2) so so 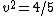
|  | shafatmubin
2009-11-03 13:55:26 | For the physics GRE, consider memorising the gamma-v relativistic table:
v = 0.999c -> gamma ~23
v = 0.995c -> gamma ~10
v = 0.99c -> gamma~7
v = 0.98c -> gamma~6
v = 0.97c -> gamma~5
v = 0.96c -> gamma~4
v = 0.95c -> gamma~3
v = 0.9c -> gamma~2.2
v = 0.85 -> gamma~2
v = 0.8c -> gamma = 5/3=1.67
I spent a while on Mathematica to figure these out. But it was worth the effort - I could guess the answer by looking at the gamma required (gamma=7/3 -> v~0.9 i.e v=Sqrt(4/5) )
jack238
2010-04-04 10:08:06 |
How could you quickly tell that gamma is 7/3?
|
|  | ams379
2009-10-07 10:46:45 | I found an easier way to do this problem.
Just use L=L_o/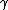
where L=vt=v(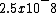 )= )=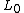 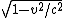
then just plug in the values:
(2/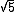 ( (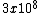 )( )(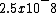 )= 15 )= 15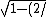 \sqrt{5} \sqrt{5}/c^2})
15/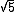 =15/ =15/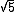 |  | ams379
2009-10-07 10:29:28 | I found an easier way to do this problem. Just use the length contraction equation. L=Lo Gamma
Where L=vt =(2.5x10^-8)v=15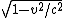
and just plug in the numbers.
(2.5x10^-8)(2/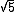 (3x10^8)=15 (3x10^8)=15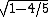
15/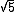 =15/ =15/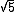 |  | shartacus
2008-08-06 12:52:58 | I think we can save ourselves some hairy arithmetic by using a little logic: Choices (D) and (E) are obviously not correct and can be eliminated.
Assume for the moment that the mesons are traveling at about c. Then, ignoring relativity for the moment, the time for the beam to reach the detector is 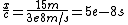
Notice that this is 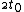 . This means that . This means that 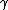 , the relativistic factor, must be at least 2, since time in the frame of the mesons must be slowed by at least a factor of two for half of them to reach the detector. Gamma stays close to 1 until v is about .8c or .9c, where it increases asymptotically. Thus, choices (A) and (B) are too low. Only (C) remains. , the relativistic factor, must be at least 2, since time in the frame of the mesons must be slowed by at least a factor of two for half of them to reach the detector. Gamma stays close to 1 until v is about .8c or .9c, where it increases asymptotically. Thus, choices (A) and (B) are too low. Only (C) remains.
In a nutshell, relativistic effects are large, so pick the choice that is closest to c without being greater than or equal to c.
Hope you guys followed my logic. This is the messed up way I think of things.
resinoth
2015-09-18 19:24:11 |
Exactly. The dilation factor is 2, which corresponds to about 0.85c. Just learn a simple table of these values.
|
|  | Mexicana
2007-10-03 18:06:00 | The second easiest way to solve this, after 'banana's solution' (which is reeeally nice btw!) is just to simply solve for  , getting , getting 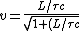^2)}} ) and then just do the ratio and then just do the ratio 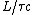 , which is reeally easy to calculate since the lifetime is given in units of , which is reeally easy to calculate since the lifetime is given in units of 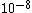 and and 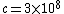 .... Hence, the nice ratio of .... Hence, the nice ratio of 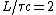 exact. exact.
HaveSpaceSuit
2008-10-16 21:13:37 |
Mexicana, I think that there is a unit discrepancy in your solution. It looks like it is unit-less. I think that factor of c in the numerator is not supposed to be there. Correct me if I'm wrong.
|
grace
2010-11-05 20:55:20 |
I think you miss time c.
|
|  | mm
2007-09-22 23:16:31 | Plug each choice into
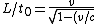^2}})
, and you can reach the answer.
|  | banana
2005-12-07 18:17:12 | Much easier: The interval is the same in all frames. Thus: 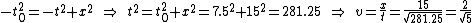
Gaffer
2007-10-27 09:47:59 |
Great soln! The math is easier if you think of it like:
The RHside
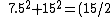^2 +15^2 = 15^2(1/4+1) = t^2)
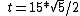
Then 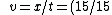 (2/sqrt{5}) )
Basically, don't multiply big numbers unless you have too. This saves time.
|
jw111
2008-11-05 12:53:37 |
Similar way(c=1)
the time for travel is
t = 15/v
and t is also the half life seen on the ground
t = 7.5r
so 15/v=7.5r -> 2/v = r
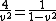
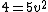
|
bac
2012-03-30 12:02:39 |
After you get to 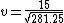 , here is how I was able to very quickly eyeball the answer. (A), (D), and (E) are obviously out.rnrnSquaring the answers (B) and (C), you get , here is how I was able to very quickly eyeball the answer. (A), (D), and (E) are obviously out.rnrnSquaring the answers (B) and (C), you get 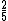 and and 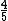 , respectively. Which one does , respectively. Which one does 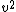 look more like? look more like? 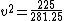 is closest to is closest to 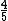 , so (C) is the correct answer. , so (C) is the correct answer.
|
|  | mg
2005-11-27 16:05:44 | The arithmetic simplifies considerably if one realizes that 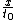 =2c. Then one has v=2c =2c. Then one has v=2c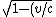^2})
fredluis721
2019-06-10 11:38:18 |
Thanks for the information on this. I really enjoy the write up. tile installer
|
|  |
|
| Post A Comment! |
You are replying to:
I think we can save ourselves some hairy arithmetic by using a little logic: Choices (D) and (E) are obviously not correct and can be eliminated.
Assume for the moment that the mesons are traveling at about c. Then, ignoring relativity for the moment, the time for the beam to reach the detector is 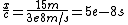
Notice that this is 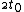 . This means that 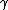 , the relativistic factor, must be at least 2, since time in the frame of the mesons must be slowed by at least a factor of two for half of them to reach the detector. Gamma stays close to 1 until v is about .8c or .9c, where it increases asymptotically. Thus, choices (A) and (B) are too low. Only (C) remains.
In a nutshell, relativistic effects are large, so pick the choice that is closest to c without being greater than or equal to c.
Hope you guys followed my logic. This is the messed up way I think of things. |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
