|
GR9677 #47
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Faraday Law }Faraday Law
Recall Faraday's Law, 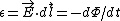 , where , where 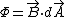 . In words, this means that a changing flux (either a varying field or radius) induces a voltage. . In words, this means that a changing flux (either a varying field or radius) induces a voltage.
The field is given as just B. The area of the loop is just 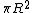 , i.e., the cross-sectional area of the cylinder. As the cylinder is spun around, its flux changes at the rate of N rps. The change in flux is thus , i.e., the cross-sectional area of the cylinder. As the cylinder is spun around, its flux changes at the rate of N rps. The change in flux is thus  , and this is the magnitude of the potential difference in choice (C). , and this is the magnitude of the potential difference in choice (C).
(Also, one can drop out the other choices from units. And, since the cylinder is moving in a magnetic field, the non-zero flux demands a voltage, so (A) can't be it.)
|
|
|
Alternate Solutions |
juliano lorenso
2014-10-11 17:43:18 | Since the wire is rotating, the charges inside the wire are also rotating and thus the B flux is going to change.
Thus d(flux)/dt does NOT equal zero, so A is WRONG |  | flyboy621
2010-10-24 16:36:45 | We can write 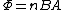 , where , where  is the number of turns in the wire (a function of time), B is the constant field, and A is the constant area of each turn of the wire. Then we have is the number of turns in the wire (a function of time), B is the constant field, and A is the constant area of each turn of the wire. Then we have
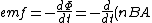=-BA\frac{dn}{dt})
But we are given .) |  | ramparts
2009-09-26 12:01:14 | Units and limits are your friend. As yosun says, you can drop B and E because of units, and A for physical reasons, but that leaves D in addition to C. *Now* you take limits ;) As the number of coils goes to 0, does the voltage vanish or blow up? Not blowing up seems like a good bet - so pick C. |  |
|
|
Comments |
ThisTestIsCancer
2018-10-21 04:21:48 | Conceptually, I\'m not a fan of this question; it seems to confound EMF (a quantity arising due to the non-zero curl induced in the E-field) with potential difference (difference in scalar field evaluated at two points), in a way that kind of felt like a trap (i.e. I was tempted to pick A).\r\n\r\nTo illustrate my point, think of a closed wire loop without any components except for some internal resistance. We can induce a current with a varying magnetic field, but there\'s not really a well-defined (or at least path-independent) potential difference between 2 points in the circuit - even for a single point, the integral  depends on how many times my path loops around the circuit.\r\n\r\nAm I correct in thinking this question is flawed for asking about potential difference rather than EMF, or is my pedantry unjustified? depends on how many times my path loops around the circuit.\r\n\r\nAm I correct in thinking this question is flawed for asking about potential difference rather than EMF, or is my pedantry unjustified?
ThisTestIsCancer
2018-10-21 04:23:35 |
Sorry about the poor formatting. It looked fine in the preview...
|
|  | whereami
2018-04-05 22:44:42 | i think the hardest part of this problem is to read it correctly. the wire is BEING wound around the the cylinder. |  | juliano lorenso
2014-10-11 17:43:18 | Since the wire is rotating, the charges inside the wire are also rotating and thus the B flux is going to change.
Thus d(flux)/dt does NOT equal zero, so A is WRONG |  | sina2
2013-09-24 10:23:09 | I really feel bad about this question. Maybe I'm wrong. But I think this question forgets to call some more details. I think we need the number of loops first, I think it should be determined that the question is about the maximum potential difference or not.
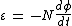
and
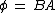
and finally
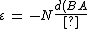 }{ dt })
If we suppose the B or loops rotate with a angular speed equal to  (I supposed the loops number is 1) (I supposed the loops number is 1)
then, we have
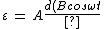 }{dt })
as a consequence
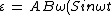)
If we're gonna to calculate the maximum induced potential, it's enough to know just non-sinusoidal part. It mentioned we have N rotation in 1 second. That means our frequency is N. The part confused me is indeed here.

and I got this as answer:
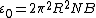
sina2
2013-09-24 10:32:13 |
OK, I see my fault. The rotation direction is matter.
|
|  | GottaMake900
2011-11-10 08:34:39 | Physically, we can intuit that there is a potential difference so A is wrong. Unit analysis provides the rest. From Faraday's law we know that EMF has the same units as Magnetic Flux per Time. Since B has units of Magnetic Field,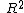 has units of Area, and N has units of Reciprocal Time, we are looking for some combination that multiplies all three of these. Choice C is the only one to fit the bill. has units of Area, and N has units of Reciprocal Time, we are looking for some combination that multiplies all three of these. Choice C is the only one to fit the bill. |  | flyboy621
2010-10-24 16:36:45 | We can write 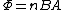 , where , where  is the number of turns in the wire (a function of time), B is the constant field, and A is the constant area of each turn of the wire. Then we have is the number of turns in the wire (a function of time), B is the constant field, and A is the constant area of each turn of the wire. Then we have
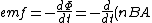=-BA\frac{dn}{dt})
But we are given .)
ewcikewqikd
2014-07-13 18:26:42 |
Thank you! rnI was so confused because I remember the formula:rnrn rnrnBut rnrnBut 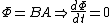 rnrnThank you for clarifying that the flux in the formula is supposed to be rnrnThank you for clarifying that the flux in the formula is supposed to be 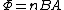 which make it which make it 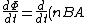 = - BA \frac{dn}{dt}) rnrn rnrn
|
zengwl17206
2017-09-13 17:55:13 |
dn/dt = 0 in your case
|
|  | South92
2009-10-20 07:52:11 | This solution is reasonable, but it seems strange that the charges on the wire do not feel the Lorentz force in the direction of the wire. Instead, the Lorentz force appears to point radially. |  | ramparts
2009-09-26 12:01:14 | Units and limits are your friend. As yosun says, you can drop B and E because of units, and A for physical reasons, but that leaves D in addition to C. *Now* you take limits ;) As the number of coils goes to 0, does the voltage vanish or blow up? Not blowing up seems like a good bet - so pick C. |  | plapas
2009-04-01 13:17:02 | This excercise is tricky enough. The magnetic field does not change, thus the E =-dΦ/dt form cannot be used, since the magnetic flux through the section that is wounded around the cylinder does not change. However, the is an induced emf due to the rotation of the segment of the wire that is parallel to the one of the cylinder's base (that then continues along the axis of the cylinder - this section can be treated as a small rod rotating perpendicular to the lines of magnetic flux). Thus we can use the faraday law is the form E =Line Integral[(uxB) *dl], for the forementioned segment. If one thinks carefully, they can see that all other segments does not contribute because they lead to zero line integral... . The answer is (C).
Prologue
2009-10-20 23:21:57 |
Excellent catch! This is so true.
|
Prologue
2009-10-20 23:54:00 |
Although I am not sure this is a form of Faraday's law. It looks to me like this:
Start with
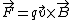
Then do a path integral on both sides
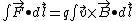
Divide the equations by q
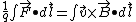
Then recognize that the left hand side is just an electric potential so that
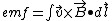
Now we want to integrate just along that little kink that is flat against the end of the cylinder, the integral will go from 0 to R. The velocity of rotation and B are perpendicular and the lorentz force is along the wire so the force is along the wire, then dotted with dl (again along the wire so it is actually dr) it just gives
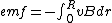
The negative sign is because of the opposition of our chosen dl to the lorentz force, in other words if we choose to go from 0 to R then our dl is in the opposite direction of the force on a positive ion in the wire.
But we can look at  as as 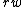 and and 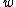 is given by is given by 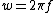 where in the case where in the case 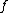 is is 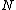 . So . So 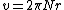 where r is a variable. Then where r is a variable. Then
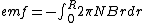
Doing the integral you get
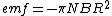
which is the answer apart from the negative sign, but you can just choose to do the path integral the opposite direction and it will be positive. In other words switch your voltmeter cords!
|
carle257
2010-04-04 22:58:41 |
The standard  does work because flux is B x total area which is does work because flux is B x total area which is  (\pi R^2)) . Then the time derivative must also differentiate number loops as a function of time. This is given as N in the problem so the total flux derivative is . Then the time derivative must also differentiate number loops as a function of time. This is given as N in the problem so the total flux derivative is 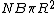 . .
|
plapas
2011-08-03 13:19:16 |
@carle257rnrnN is not the number of loops but the revolutions of the cylinder per second (many people interpret the problem as increasing number of loops around the circumference of the cylinder ... but my perspective is this: in the first line the problem describes how wire is attached to the cylinder ... afterwards the whole system is placed in a magnetic field and rotates (with the wire fixed on the cylinder's surface). Why do people think that the wire is wound around the cylinder while inside the magnetic field? It is not at all implied in the problem ...
|
plapas
2011-08-03 13:22:10 |
@ prologue you got the point ... you gave the analytic solution of the problem!
|
maxdp
2013-09-26 09:21:47 |
I'm going to have to disagree with plapas. As other people have mentioned, the wording of the problem says the wire is "being wound" around the cylinder. Thus the total flux is changing. If the wire were not being wound, the flux would not change at all, and the answer would just be (A).
|
kronotsky
2018-10-22 02:50:28 |
One way to see that this idea must be wrong is that the system would then have a discrete time symmetry. If there were an induced emf, this would result in resistive charge transport down the wire and a non-periodic change in charge distribution, violating the symmetry.
|
|  | sharpstones
2007-08-11 15:34:25 | Ah!! Now I understand!
The key here is that the wire is BEING wound around the rotating wooden cylinder during the whole time. So as it spins around more and more of the wire is wound around the cylinder and hence more flux is enclosed by the whole wire!
plapas
2009-08-05 10:04:20 |
THIS IS A WRONG APPROACH. THE EXERCISE DOES NOT MENTION THAT THE WIRE GRADUALLY WOUNDS AROUND THE CYLINDER. THERE IS SOME PORTION WOUNDED AROUND THE CYLINDER AND THE REST OF THE WIRE DIRECTS ALONG THE AXIS OF SYMMETRY. THE SOLUTION GIVEN ABOVE IS ALSO WRONG!!!
|
Wildroses
2009-09-20 13:31:20 |
Actually, the problem does state that it is gradually being wound.rnrn"A wire is BEING wound around a rotating wooden cylinder".
|
wittensdog
2009-10-30 19:43:44 |
all caps =/= correctness
|
FutureDrSteve
2011-11-03 13:19:55 |
"the cylinder is placed in a uniform magnetic field of magnitude b parallel to its axis and rotates at n revolutions per second." i'd say that pretty strongly implies that the number of loops on the solenoid is increasing with time, and therefore, so is the flux.
all lowercase == correctness :P
|
drg
2012-06-06 19:08:12 |
I think he's got a point. After the first rotation, the wire is wound once around the wooden cylinder, and Φ = πR²B. After 2 seconds, the wire is wound twice, and Φ = (2)πR²B etc. so that in general Φ(t) = Nt*πR²B
Then |emf| = |dΦ(t) / dt| = πNBR²
|
drg
2012-06-06 19:11:30 |
*CORRECTION: after the first SECOND, the wire is wound N times around the wooden cylinder, so Φ = NπR²B, after t=2sec, Φ = (2)NπR²B etc. and thus in general Φ(t) = Nt*πR²B
|
|  | sharpstones
2007-04-05 05:33:49 | Yea, I don't understand either. As far as I can tell the flux is constant regardless of whether the cylinder is rotating or not. |  | RebeccaJK42
2007-03-18 18:39:25 | Around which axis is the cylinder rotating? The way I pictured the problem, I don't see how the flux changes at all...
tmsc
2015-04-12 05:51:11 |
The key point is that the wire is being wound around the cylinder. For every turn of the cylinder, the area exposed to the magnetic field increases in 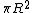 . Since the area is changing, we have a change of flux that makes a voltage across the wires, per Faraday's law . Since the area is changing, we have a change of flux that makes a voltage across the wires, per Faraday's law
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
