|
GR9677 #43
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
enterprise
2018-04-01 15:56:18 | The z direction don\'t contribute because it\'s perpendicular. The remaining vector is the derivative of the radial unit vector multiplied by an R. This is the angular unit vector. Another factor of R comes in from 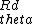 |  | Awardr
2017-09-14 20:15:29 | No integral needed. If you plot out he vectors along the axes you realize that they point in a circle. At radius R the vector magnitude is R so your line integral around the circle is 2*pi*R * R = 2piR^2 |  | flyboy621
2010-10-24 15:42:47 | In hindsight (always 20/20):
Yosun's approach is good, but there is a shortcut once you decide to integrate over the area instead of the perimeter. Since the circle is in the x-y plane, you can see that the normal is always 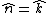 , so only the , so only the 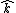 component of the curl will contribute to the integral. You don't even need to calculate the other components of the curl (even though in this problem they turn out to be zero anyway). component of the curl will contribute to the integral. You don't even need to calculate the other components of the curl (even though in this problem they turn out to be zero anyway).
Now you know that the answer is just the magnitude of the z-component of the curl, multiplied by the area of integration, or 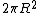 . . |  | CarlBrannen
2010-10-07 14:27:08 | u = (y, -x, z). On a circle of radius R in the x-y plane. So z=0, ignore the z-component. The required integral is:
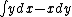 . .
In polar coordinates we have
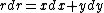 and and 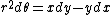 . .
So convert to polar coordinates. Get:

This is closest to (C), but with a sign error. Evidently they went around the circle in the negative direction so choose (C).
eric t
2010-10-07 23:43:18 |
Alternatively, use Green's theorem on your line integral rn(=\int\int_{D}(B_{x}-A_{y})dx dy=\int\int_{D}-2dx dy=-2\pi R^{2}) ). ).
|
Clay
2012-04-30 05:53:45 |
Green's theorem method is the easiest.
|
|  | t-k-n-o
2008-06-21 14:29:12 | I really think that is easier to do the line integral. in this case is:
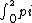 R(cost,-sint)R(cost,-sint)dt=2pi R(cost,-sint)R(cost,-sint)dt=2pi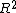
t-k-n-o
2008-06-21 15:57:26 |
The line integral is:
 \right) . a ^{\prime }\left( t\right) dt)
Where  =\left( \sin t,\cos t,0\right) ,) and and  =\left( y,-x,z\right) )
then,
 \cdot R\left( \cos t,-\sin t,0\right) dt=2\pi R^{2})
|
|  | Jeremy
2007-11-07 17:28:17 | 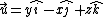
![\nabla \times \vec{u}=[\partial_{y}(z)-\partial_{z}(-x)]\hat{i}-[\partial_{x}(z)-\partial_{z}(y)]\hat{j}+[\partial_{x}(-x)-\partial_{y}(y)]\hat{k}](/cgi-bin/mimetex.cgi?\nabla \times \vec{u}=[\partial_{y}(z)-\partial_{z}(-x)]\hat{i}-[\partial_{x}(z)-\partial_{z}(y)]\hat{j}+[\partial_{x}(-x)-\partial_{y}(y)]\hat{k})
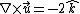
There should be no confusion about the sign at this point because all of this is just by definition. The part to be cautious on is the convention for area vector direction in this integral:
 \cdot d\vec{a}) , ,
over a circle of radius 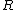 in the in the 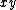 -plane whose center is at the origin. (The -plane whose center is at the origin. (The 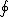 symbol is meant for closed surfaces - like spherical shells; it is not appropriate in this case). The integral is simplified as follows: symbol is meant for closed surfaces - like spherical shells; it is not appropriate in this case). The integral is simplified as follows:
 \cdot d\vec{a}= -2\hat{k} \cdot \int d\vec{a}=-2 a (\hat{k} \cdot \hat{a})=-2 \pi R^{2} (\hat{k} \cdot \hat{a})) . .
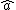 is ambiguous here because the direction of integration around the circle is not specified. However, given the direction of integration, you would use the right-hand rule to find the direction of is ambiguous here because the direction of integration around the circle is not specified. However, given the direction of integration, you would use the right-hand rule to find the direction of 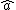 , your fingers follow the circular path and your thumb gives the direction of , your fingers follow the circular path and your thumb gives the direction of 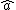 . For . For 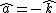 , and therefore the proper sign in the answer, I think the path would be clockwise, i.e. starting on the , and therefore the proper sign in the answer, I think the path would be clockwise, i.e. starting on the 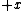 axis, you would first cross the axis, you would first cross the 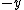 axis, then the axis, then the 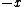 axis, then the axis, then the 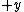 axis, and then return to where you started on the axis, and then return to where you started on the 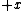 axis. Of course, the answer choices only differ in magnitude, so you could be much sloppier on the test and come away unscathed, but I still think it's good to be aware of the finer details. axis. Of course, the answer choices only differ in magnitude, so you could be much sloppier on the test and come away unscathed, but I still think it's good to be aware of the finer details.
infiniteseries
2008-11-05 17:36:51 |
Thanks for posting this.
|
|  | ray
2007-09-22 15:36:00 | shouldn't the answer be 0 since u can be written as a gradient of some function f = (yx, -xy, z^2/2) ?
Blake7
2007-09-23 05:24:34 |
The answer to your question, Ray, is "No".
Perhaps you're thinking Curl(Grad(func.))=0. That's not what we're talking about at all here.
Try this.
Set up the determinant for curl(u) here and find your way to curl(u) = 2 (or -2) Then, look at the Stokes theorem like Yosun says, take into acount the area of the closed circular path, and get to 2PiR^2 (or -2PiR^2) for answer (C).
Fortunately, they didn't throw in -2PiR^2 as a choice on this one! => I think that Santon is correct about the direction one goes around the line integral.
|
Gaffer
2007-10-26 22:35:53 |
Ray was thinking of the definition of a conservative force: namely one that can be described as the gradient of a potential. 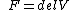 The integral around a closed loop for a conservative force is zero. No work is done or energy lost and hence the name "conservative." The integral around a closed loop for a conservative force is zero. No work is done or energy lost and hence the name "conservative."
Think gravity. You can always pick up something you drop - return its gravitational potential energy. The PE is not "lost".
The function in this case is not conservative since there is no single scalar function whose derivative (or 3-D derivative the gradient) equals u. Notice how each of Ray's funcitons were correctly integrated, but different from each other. Also, he expressed it in coordinate form, ie with vector quality. This is also incorrect. the potential is a scalar function. The gradient of a scalar field is a vector.
|
|  | cyberdeathreaper
2007-01-17 17:58:48 | Could someone expand on the entire calculation? There seems to be some confusion with the signs, and I'm confused by santon's remarks (wouldn't -2k dotted with some positive value in the k direction still give a negative result?)
Richard
2007-09-23 22:21:48 |
The curl gives a negative 2. Then assuming a clockwise loop, there is an area with a normal pointing in the -z direction. The two when multiplied give a positive result. In any case, it doesn' t really matter which way you decide to go around the loop, since there is only one answer with the correct magnitude.
|
flyboy621
2010-10-24 15:32:23 |
Just to clarify, the curl is 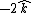 , which fortunately for us is parallel to our , which fortunately for us is parallel to our 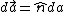 of integration. Or antiparallel if you prefer--either way you can quickly see that integrating over the area of the circle will just give the magnitude of the curl times of integration. Or antiparallel if you prefer--either way you can quickly see that integrating over the area of the circle will just give the magnitude of the curl times 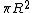 . If you get a negative sign, don't worry about it since they didn't specify a direction of integration. . If you get a negative sign, don't worry about it since they didn't specify a direction of integration.
|
|  | santon
2006-11-03 07:04:36 | I get -2 also, but I think it's ok. If you take a counterclockwise circle, then da points in the positive z hat direction. Then the dot product cancels the minus sign. So I guess this corresponds to a counterclockwise loop?? |  | radicaltyro
2006-11-02 21:06:26 | I am getting _z=-2) . . |  | Richard5784
2006-09-16 10:13:54 | I think you are evaluating the line integral over the z-axis, so to avoid confusion it should be written (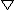  u) u) = 2 = 2
Prologue
2009-10-20 22:43:51 |
No matter how you look at it the curl for this field is -2k hat. That is the curl period. There are no other components.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
