|
GR9677 #42
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Photoelectric Effect }Photoelectric Effect
Recall the photoelectric equation relating the incident electromagnetic wave to the kinetic energy and the work function 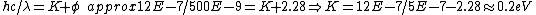 , as in choice (B). , as in choice (B).
|
|
|
Alternate Solutions |
cczako
2013-10-18 15:36:40 | Remember KE=E-phi where E is the energy of the light and phi is the workfunction. Don't forget that E=hc/lambda and that hc can be written as 1240 nm*eV. That means that 500 nm is about 2.5 eV so KE is simply 2.5 -2.28 which is 0.22 eV or choice B. |  |
|
|
Comments |
cczako
2013-10-18 15:36:40 | Remember KE=E-phi where E is the energy of the light and phi is the workfunction. Don't forget that E=hc/lambda and that hc can be written as 1240 nm*eV. That means that 500 nm is about 2.5 eV so KE is simply 2.5 -2.28 which is 0.22 eV or choice B. |  | Dodobird
2010-11-12 14:46:11 | We get E = .12 eV, which doesn't really help us differentiate between choice A and B. There is a difference of .01 eV in 'closeness' to these answers. In fact the wording of the problem would suggest our maximum energy can only be .03 eV out of the choices given.
Help?
pam d
2011-09-15 21:55:01 |
I know this is way too late but you actually get 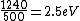 (a reasonable mental calculation). The difference between this and the work function gives the maximum possible KE, which puts you at about (a reasonable mental calculation). The difference between this and the work function gives the maximum possible KE, which puts you at about 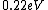 . .
|
|  | CarlBrannen
2010-10-07 14:14:11 | Use h-bar c = 1240 nm eV. Converting 500nm, we get 2.48 eV. Subtracting 2.28 eV for the work function, we find 0.2 eV, answer (B). |  | vortex
2005-12-05 15:50:02 | As a twist of fate!, the formula is given in question 27. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
