|
GR9677 #14
|
|
|
|
|
Alternate Solutions |
Sagan_fan
2013-05-21 09:16:15 | This can be done in about 10 seconds if one recalls calorimetry. For insulated objects in contact that come to thermal equilibrium: Q lost = Q gained.
Given the blocks are identical, the magnitude of temperature change is the same for both, so Q lost (or gained) = mC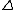 T = 0.1 kC/K*50 K = 5 kC T = 0.1 kC/K*50 K = 5 kC |  |
|
|
Comments |
Sagan_fan
2013-05-21 09:16:15 | This can be done in about 10 seconds if one recalls calorimetry. For insulated objects in contact that come to thermal equilibrium: Q lost = Q gained.
Given the blocks are identical, the magnitude of temperature change is the same for both, so Q lost (or gained) = mC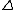 T = 0.1 kC/K*50 K = 5 kC T = 0.1 kC/K*50 K = 5 kC |  | Barney
2012-11-06 02:11:24 | So why does one take for mass only 1kg and not 2kg?
I think both bodies are involved in heat transfere once in contact?
someguy
2012-11-08 15:11:03 |
You're only looking at the energy needed to heat the one block (the one at a lower temperature) since heat "flows" from high temp to low temp, so you calculate the energy using only the colder block and it's specific heat and the change in it's temperature
|
|  | Phys4
2010-08-02 15:44:18 | Curious, the version of the exam I have (GR9677 obtained from the Ohio State website) defines the specific heat in units of Kelvin and not Celsius. To compute this problem straight through, I would believe that you would need to convert from Celsius to Kelvin. In this case, since you don't, am I safe to assume that the original exam had an error?
gravity
2010-09-24 22:41:01 |
It's the same thing. You do need to convert to absolute temperature in most cases, but the equation for is Q=mc∆T. The ∆T is the same whether you're using degrees celsius or kelvins (100℃ - 0℃) = (373K - 273K) = 100K
Even with all of that said, the units are per degree. A kelvin is the same as a degree of Celsius and so they are exactly the same.
|
edschiap
2012-02-28 05:21:00 |
I think that there is a serious mistake becuase the specific calor has units in ēKelvin. Then, the difference of temperatures must be in ēKelvin. Namely:
mass [Kg] * ) [Kelvin] * c [Kcal/ēKelvin Kg] = [Kelvin] * c [Kcal/ēKelvin Kg] =
Q [Kcal]
And the diferrence of temperature in kelvin es 323 and in celsius is 50.
That is all.
|
edschiap
2012-02-28 05:29:17 |
I am sorry I made a mistake in my last coment. The equilibrium temperature is different if you work in kelvin or celsius, but the difference of the temperature (and this is what is important!) is the same. I am sorry.
|
|  | wittensdog
2009-10-16 14:18:22 | Just a little side note, which may or may not have been implicitly assumed here in the solution (I'm not sure which way was used to attain the value of fifty degrees). Whenever you have two identical bodies, the resulting temperature is the average of the initial ones. It would be very nice of ETS if all of their problems had nice little features like this, but I certainly wouldn't count on it! In general you would need to use,
m1*c1*(T1 - Tf) + m2*c2*(T2 - Tf) = 0
and then solve for Tf. Then you can plug Tf back into one of the two terms above to find the heat transfer. |  | Ning Bao
2008-01-30 10:19:22 | Dimensional Analysis:
They give you a constant that has units A/BC. Average the two temperatures to get something of units C. B is given. Multiply for the win.
JMOAN
2008-10-30 20:33:54 |
Just a warning on Ning Bao's comment:
This assumes that there aren't other attributes to the solution (such as multiplication by a scaler), which happens to be true for this problem, but is not always the case. In general, we can only use simple dimensional analysis to eliminate answers that have the wrong dimensions (this problem's solutions all have the same dimensionality). Otherwise, you might think that kinetic energy, which has units of  , is just calculated by multiplying mass by the square of velocity, when in fact you must multiply this result by 0.5: , is just calculated by multiplying mass by the square of velocity, when in fact you must multiply this result by 0.5: 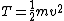
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
