|
GR9277 #97
|
|
|
Problem
|
|
\prob{97}
Lattice forces affect the motion of electrons in a metallic crystal, so that the relationship between the energy E and the wave number k is not the classical equation 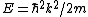 , where m is the electron mass. Instead, it is possible to use an effective mass , where m is the electron mass. Instead, it is possible to use an effective mass 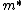 given which of the following? given which of the following?
-
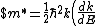$)
-
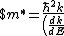}$)
-
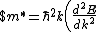^{1/3}$)
-
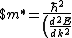}$)
-
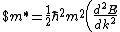$)
|
Advanced Topics }Solid State Physics }Solid State Physics
This is a result one remembers by heart from a decent solid state physics course. It has to do with band gaps, which is basically the core of such a course.
Then again, one can easily derive it from scratch upon recalling some basic principles: =\hbar^2 k^2/(2m)) , ,  , where k is the wave vector, E is the energy, m is the mass, and p is the momentum. , where k is the wave vector, E is the energy, m is the mass, and p is the momentum.
From the above, one has 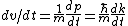 . .
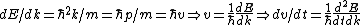
Set the two 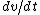 's equal to get 's equal to get  . Cancel out the . Cancel out the  's to get 's to get 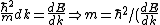) , after differentiating with respect to k on both sides. , after differentiating with respect to k on both sides.
Alternatively, one can try it Kittel's way:
Start with 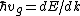 . Then, . Then, 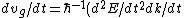= \hbar^{-1}(d^2E/dt^2F/\hbar)) . Thus, the effective mass is defined by . Thus, the effective mass is defined by 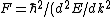 dv_g/dt=mdv_g/dt) . .
|
|
|
Alternate Solutions |
drdoctor
2013-09-17 08:48:06 | Here's how I solved the problem:
Presumably, you want m* to be written in terms of some sort of constants--ie. m* shouldn't depend on k or E explicitly. However, 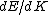 or or 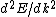 could potentially be constants, so they could be included in m*. So, that eliminates A, B, and C. It's fairly easy to see from here that answer D is simply the second derivative of E with respect to k for the equation given in the problem statement, except that you need to rearrange to solve for m after taking the double derivative: could potentially be constants, so they could be included in m*. So, that eliminates A, B, and C. It's fairly easy to see from here that answer D is simply the second derivative of E with respect to k for the equation given in the problem statement, except that you need to rearrange to solve for m after taking the double derivative:
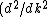E = \hbar^2/m)
Therefore:
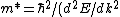)
You could also use units to eliminate E. |  | jonestr
2005-11-12 00:50:59 | a quick dimnesional analysis wors well here
|  |
|
|
Comments |
honeybunches
2016-09-12 20:04:35 | Here is a quick approach: If the dispersion relationship was the classical equation, we would expect the effective mass to be equal to the electron mass. This very quickly gets you (D) |  | sina2
2013-10-08 04:01:01 | I will chose D. I'm always caring to not forget in quantum 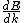 isn't same is isn't same is 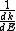 . This is so important. They maybe don't commute. . This is so important. They maybe don't commute. |  | drdoctor
2013-09-17 08:48:06 | Here's how I solved the problem:
Presumably, you want m* to be written in terms of some sort of constants--ie. m* shouldn't depend on k or E explicitly. However, 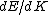 or or 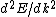 could potentially be constants, so they could be included in m*. So, that eliminates A, B, and C. It's fairly easy to see from here that answer D is simply the second derivative of E with respect to k for the equation given in the problem statement, except that you need to rearrange to solve for m after taking the double derivative: could potentially be constants, so they could be included in m*. So, that eliminates A, B, and C. It's fairly easy to see from here that answer D is simply the second derivative of E with respect to k for the equation given in the problem statement, except that you need to rearrange to solve for m after taking the double derivative:
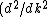E = \hbar^2/m)
Therefore:
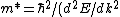)
You could also use units to eliminate E. |  | nitin
2006-11-21 00:45:56 | Let 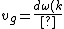}{dk}) be the group velocity of the electron. Then be the group velocity of the electron. Then
}{dk}\right)) , and , and
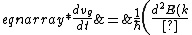}{dk^2}\frac{dk}{dt}\right)\\&=&\frac{1}{\hbar}\left(\frac{d^2E(k)}{dk^2}\right)\left(\frac{1}{\hbar}\frac{dp}{dt}\right)\\&=&\frac{1}{\hbar}\left(\frac{d^2E(k)}{dk^2}\right)\left(\frac{m^*}{\hbar}\frac{dv_g}{dt}\right),\end{eqnarray*})
where  is the effective mass. The answer (D) follows. is the effective mass. The answer (D) follows. |  | comorado
2006-10-27 13:07:45 | You wrote 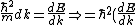)
Must be: 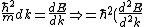) |  | jonestr
2005-11-12 00:50:59 | a quick dimnesional analysis wors well here
Jeremy
2007-11-03 15:33:07 |
Dimensional analysis will only narrow it down to choices (A) and (D).
|
Poop Loops
2008-10-25 20:39:17 |
Yeah, but then there's a 1/2 out front, which doesn't make sense.
|
ramparts
2009-08-06 23:30:04 |
Yep - it's possible I screwed something up (and I didn't bother looking at E after I looked at A through D :P) but I'm pretty sure the first three were not units of mass.
|
alemsalem
2010-09-26 08:28:20 |
you might reason that the mass shouldn't be dependent on momentum (k) otherwise it wouldn't be useful to use an "effective mass" so it cannot be A.
but i admit when i did the exam i solved this one based on units then just picked A as a guess
|
flyboy621
2010-10-23 05:26:41 |
Sort of, but that only narrows it down to A or D. Of course it's worth guessing at that point...
|
asdfuogh
2011-10-05 19:04:12 |
I would pick D) if I had to pick from A) and D)... A) looks like the original mass equation, except with differentials. Not a great reason, but still..
|
eighthlock
2013-09-15 12:39:01 |
Dimensional analysis does not distinguish between options (A) and (D)
|
|  | jonestr
2005-11-12 00:50:06 | |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
