raytyler
2018-11-01 03:14:57 | \\lambda_1 = -\\frac{1}{2} + i\\frac{sqrt{3}}{2}\r\n\r\n\\lambda_2 = -\\frac{1}{2} - i\\frac{sqrt{3}}{2}\r\n\r\n\\lambda_3 = 1\r\n192.168.0.1 http://19216801help.com/
amandawallers
2019-05-23 04:09:55 |
I have done exactly what you guys have told but the result is not the same and I dont know why.\r\nHill climb racing
|
|  |
raytyler
2018-11-01 03:13:02 | 1 + i - i is not equal to 0. The eigenvalues are actually 1, -\\\\\\\\\\\\\\\\frac{1}{2} \\\\\\\\\\\\\\\\pm \\\\\\\\\\\\\\\\frac{\\\\\\\\\\\\\\\\sqrt{3}}{2}i.\r\n192.168.0.1 login |  |
Benjamin
2018-08-08 07:15:11 | Hi there tim\r\n\r\n[url=http://www.pumpkin.com]harry[/url] " target="_blank">http://www.tim.com\">tim\r\n\r\n[url=http://www.pumpkin.com]harry[/url] \r\n\r\nhttp://www.essaywritinglab.co.uk/ |  |
blabla0001
2017-03-25 09:10:25 | Notice that the char. equation for this matrix is 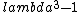
blabla0001
2017-03-25 09:11:29 |
Sorry about this. everything is fine
|
|  |
neo55378008
2012-08-18 13:26:23 | Some simple matrix properties should help.
The trace of a matrix is invariant, so 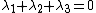
The determinant is also equal to the product of the eigenvalues (1 in this case)
All real eigenvalues of one would give the right determinant, but the wrong trace!
Using 1, i, and -i both the trace and determinant are correct.
TheBridge
2018-10-27 02:12:16 |
But 1 + i - i is not equal to 0. The eigenvalues are actually 1, 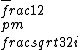 . .
|
|  |
fizix
2010-11-09 17:49:37 | By spectral theory only a symetric matrix have a full real eigenbasis. This matrix is not symetric
shka
2018-07-03 15:22:19 |
fizix has asserted the converse of the spectral theorem, which is not true in general. In fact, it\'s easy to find a non-symmetric diagonalizable real matrix. For example,\r\n\r\n[ 5 -4 ] \r\n[ 4 -5 ] \r\n\r\nis ANTI-symmetric but has eigenvalues 3 and -3. The spectral theorem guarantees the diagonalizability of real symmetric matrices, but it does not force all diagonalizable real matrices to be symmetric.
|
|  |
neutrinosrule
2008-10-05 20:21:41 | once you have the characteristic equation, you can note that the only possible real root is 1... therefore the other two roots must be imaginary (since a third order polynomial must always have 3 roots). No need to waste time finding the roots. |  |
blah22
2008-04-11 18:59:32 | Out of curiosity is it OK to say since it is not hermitian it's eigenvalues aren't real?
chrisfizzix
2008-10-14 13:24:31 |
I agree; this test is about physics, and the physical result that corresponds to this question is from quantum mechanics. Only Hermitian matrices give you observables - that is, all real eigenvalues. This matrix is not Hermitian, easily seen as it is real but not equal to its transpose. Thus, the statement that all its eigenvalues are real is clearly false.
|
student2008
2008-10-16 15:18:47 |
You're not quite right. Although Hermitian matrices definitely have only real eigenvalues (and the orthonormal basises composed of eigenvectors), the opposite statement is erroneous. For example, the matrix
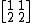
has real eigenvalues 0 & 3, but it's not Hermitian (real, but not diagonal).
|
|  |
petr1243
2008-03-15 16:46:02 | Using det(A-I ) = 0, we will simply get: ) = 0, we will simply get:
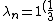) ,n=1,2,3, Solving this we get: ,n=1,2,3, Solving this we get:
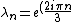) , n=1,2,3 , n=1,2,3
So: 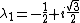
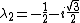
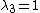
These 3 eigenvalues satisfy all choices, except for choice B.
Marie1434
2023-05-08 08:36:10 |
Nice! #post
|
Marie1434
2023-05-08 08:39:39 |
Nice! post
|
|  |
dumbguy
2007-10-10 18:11:05 | Could some one maybe post the classic why the other answers are wrong?
dumbguy
2007-10-10 18:12:48 |
I mean why the other ones are right
|
alemsalem
2010-09-26 09:04:30 |
(A) the trace is always the sum of the eigenvalues (sum of the terms on the diognal of the matrix which is 0+0+0), or you can say the trace is the same in all representations.
(E) this is just the eigenvalue equation.
for the rest substitute the roots:
1, exp(i 2 pi/3),exp(-i 2 pi/3).
hint 2*cosine(2 pi/3) = -1
|
|  |
jax
2005-12-07 11:14:12 | Where do you get 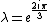 ? ?
nitin
2006-11-21 00:54:14 |
Trivial:
The characteristic equation is
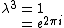 . Therefore . Therefore
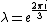 . .
|
Zephyr3.14
2007-04-07 23:25:30 |
does this work? Then wouldn't
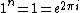
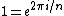
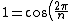 + i \sin\left(\frac{2 \pi}{n}\right))
![Re[1] = 1 = \cos\left(\frac{2 \pi}{n}\right)](/cgi-bin/mimetex.cgi?Re[1] = 1 = \cos\left(\frac{2 \pi}{n}\right))
so
 = 1 \ \ \forall \theta) ? ?
Why isnt it just 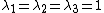 ? ?
|
Richard
2007-09-13 14:45:46 |
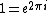
^n=(e^{2\pi{i}})^n=e^{2\pi{in}} \hspace{1cm}\forall{n}\in{N})
Putting Euler to work,
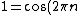+i\sin(2\pi{n})) . .
But because, =0 \forall{n}\in{N})
and =1 \forall{n}\in{N}) , ,
you really don't arrive at anything that interesting.
|
jburkart
2007-11-02 00:45:49 |
In a complex analysis course you will learn about branch cuts and how you have to be careful with roots. I can also prove the following: 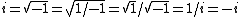 . Where's the error? . Where's the error?
|
Jeremy
2007-11-03 16:13:17 |
Link
|
Ryry013
2019-10-19 13:09:20 |
New link: http://uni.dougshaw.com/findtheerror/index.html
|
|  |
