|
GR9277 #96
|
|
|
|
|
Alternate Solutions |
ryanjsfx
2014-09-26 17:32:59 | The only optics equation I can think of with index of refraction in it (besides snell's law) is for a thin film:
2nt=m*lambda
(destructive interference since fringes) where t is thickness and m is the order = 40, given.
Then, n = (40*500e-9)/(2*5e-2) = 2e-4
which can't be quite right since n = 1 for vacuum, so the answer must be 1.0002
Let me know if my reasoning is really flawed and I just got lucky or if this is relatively sound. |  | faham
2006-10-26 22:33:35 | Let:
* N be the number of full wavelengths across the gas-filled cell
* N' be the number of full wavelengths across the cell when it's empty
* lambda_0 is the wavelength of light in vaccuum
* lambda is the wavelength of light in a material of index of refraction n
* d is the length of the cell (5 cm)
* M is the number of fringes seen on the screen
N = d/lambda_0
N' = d/lambda
Now, we know that lambda = lambda_0/n, so
N' = d*n/lambda_0
Be aware that the light goes IN and back OUT of the cell (it's an interferometer!), so
N' - N = M/2
Again, even though you see 40 fringes, it's 20 wavelengths that N gets shifted by.
N' - N = M/2 = d*n/lambda_0 - d/lambda_0
M/2 = d/lambda_0*(n-1)
Solving for n:
n = M*lambda_0/(2*d) + 1
n = (40)*(500nm)/(2*5cm) + 1
n = 1.0002
So the answer is C |  |
|
|
Comments |
dc771957
2016-10-19 16:14:04 | The total change in phase is: 40  \r\nThe initial optical path length in the cell is: 2Ln\'\r\nwhere n\' is the refractive index of air.\r\nThe optical path length of the evacuated cell is: 2Ln\r\nwhere n is the refractive index of a vacuum, so 2Ln=2L.\r\nThe total change in phase is equal to the change in optical path length: 40 \r\nThe initial optical path length in the cell is: 2Ln\'\r\nwhere n\' is the refractive index of air.\r\nThe optical path length of the evacuated cell is: 2Ln\r\nwhere n is the refractive index of a vacuum, so 2Ln=2L.\r\nThe total change in phase is equal to the change in optical path length: 40  = 2Ln\'-2L = 2L = 2Ln\'-2L = 2L ) \r\nSo, n\' = 40 \r\nSo, n\' = 40  /2L + 1 /2L + 1
dc771957
2016-10-19 16:24:49 |
Yo I hate this latex jaunt. The goddamn preview looked beautiful. Just disregard everything ive said. At least I tried.
|
|  | MonaJalilvand
2015-10-21 13:07:51 | If the length of the tube is L, the number of wavelengths that can be put in the tube is N=2L/lambda. After inserting the gas cell, the number of wavelengths becomes, N\\\\\\\'=( 2L-2d)/lambda+2dn/lambda, now subtract these two numbers to get, N\\\\\\\'-N= 2d/lambda(n-1).\\\\r\\\\nwe know that the change of one wavelength, changes the number of fringes by one, so N\\\\\\\'-N=40, and there we find for n=1.0002.
MonaJalilvand
2015-10-21 18:25:37 |
sorry for the fonts going messy...I don\'t know what the problem is, I hope it works now.\r\nIf the length of the tube is L, the number of wavelengths that can be put in the tube is N=2L/lambda. After inserting the gas cell, the number of wavelengths becomes, N\'=( 2L-2d)/lambda+2dn/lambda, now subtract these two numbers to get, N\'-N= 2d/lambda(n-1). We know that the change of one wavelength, changes the number of fringes by one, so N\'-N=40, and there we find for n=1.0002.
|
|  | ryanjsfx
2014-09-26 17:32:59 | The only optics equation I can think of with index of refraction in it (besides snell's law) is for a thin film:
2nt=m*lambda
(destructive interference since fringes) where t is thickness and m is the order = 40, given.
Then, n = (40*500e-9)/(2*5e-2) = 2e-4
which can't be quite right since n = 1 for vacuum, so the answer must be 1.0002
Let me know if my reasoning is really flawed and I just got lucky or if this is relatively sound.
kronotsky
2018-10-26 03:27:43 |
The relative differences in wavelengths is given by the factor (n-1), so this is what you are equating to 2e-4. Other than that, the situation happens to be exactly analogous, since increasing the index of refraction essentially increases the effective optical path length, which is the quantity used to derive the thin film equation.
|
|  | sina2
2013-10-08 03:47:20 | First find  before filling the chamber. before filling the chamber.

Now we know how much path difference would be made by filling the chamber.
We suppose after filling the chamber,  is the time to pass the chamber length by is the time to pass the chamber length by  speed. During this time in previous situation the light would pass speed. During this time in previous situation the light would pass  . So . So

 and and 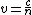
by dividing this two equation we find
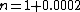 |  | Setareh
2011-11-07 11:53:27 | Hi everyone.. I have PGRE exam just 5 days later.. It is rainy now.. I hope everyone do the best in this exam..
zeper
2012-08-19 07:16:40 |
I hope you did well=)
|
|  | gravity
2010-11-05 02:31:17 | Keep in mind that it goes through the 5cm twice, and so the path length is 10cm.
Each fringe represents a wavelength being added to the path length.
The number of wavelengths in 10cm is 10cm/500nm = 2*10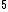 = 200,000 = 200,000
Add 40 to this, and you have the number of wavelengths in vacuum = 200, 040
Divide these two to get the index of refraction.
az
2015-04-05 15:00:40 |
This is a great way to think about this problem, but I believe gravity meant to say that there are 200,040 wavelengths in gas, not in vacuum. Since the wavelength in gas will be shorter than the wavelength in vacuum, more of them will "fit into" the 10 cm. distance the light must traverse. I believe the ratio we are taking is essentially a ratio of wavenumbers, which is the inverse of the ratio of wavelengths since k is proportional to 1 over lambda. (Sorry, no LaTeX skills.)
|
|  | BerkeleyEric
2010-06-28 20:18:36 | At this point it's likely that time is at a premium. Even if you know very little about a Michelson interferometer, the only way to get numbers in the right range is dividing lambda by the path length and then multiplying by the number of fringes. The closest thing to this is (C). |  | Imperate
2008-10-17 07:03:31 | The key here is the optical path difference, given that the mirrors dont move etc everything else is constant except the bit of path going through the gas chamber. The optical path length of this section is 0.1n [metres]. For a maxima the total path difference of the total rays must be a integer multiple of the wavelength 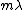 .Therefore one obtains the expression .Therefore one obtains the expression 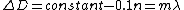 . Multiply both sides by 10, and one can see that if the optical n changes by 10 . Multiply both sides by 10, and one can see that if the optical n changes by 10  a new fringe will appear. Given that 40 fringes went past this implies a new fringe will appear. Given that 40 fringes went past this implies 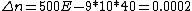 . .
The refractive index of air is 1 therefore 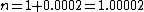 . Choice C . Choice C |  | dumbguy
2007-10-10 18:01:07 | What happened to the nanometers? Why did we choose to just leave them out? |  | faham
2006-10-26 22:33:35 | Let:
* N be the number of full wavelengths across the gas-filled cell
* N' be the number of full wavelengths across the cell when it's empty
* lambda_0 is the wavelength of light in vaccuum
* lambda is the wavelength of light in a material of index of refraction n
* d is the length of the cell (5 cm)
* M is the number of fringes seen on the screen
N = d/lambda_0
N' = d/lambda
Now, we know that lambda = lambda_0/n, so
N' = d*n/lambda_0
Be aware that the light goes IN and back OUT of the cell (it's an interferometer!), so
N' - N = M/2
Again, even though you see 40 fringes, it's 20 wavelengths that N gets shifted by.
N' - N = M/2 = d*n/lambda_0 - d/lambda_0
M/2 = d/lambda_0*(n-1)
Solving for n:
n = M*lambda_0/(2*d) + 1
n = (40)*(500nm)/(2*5cm) + 1
n = 1.0002
So the answer is C
caffeinated
2008-04-08 12:56:36 |
Why do you use lambda for N' when N' is the empty cell and lambda is lambda in the gas? I don't understand. Why wouldn't you use lambda-0 for N'?
|
|  | astro_allison
2005-11-26 22:02:48 |  ? ?
astro_allison
2005-11-26 22:17:25 |
wouldn't 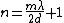 ? ?
|
yosun
2005-11-26 23:06:44 |
astro_allison: thanks for the typo-alerts; both typos have been corrected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
