|
GR9277 #95
|
|
|
|
|
Alternate Solutions |
student2008
2008-10-16 14:29:27 | One can answer the question without solving it, recalling that the typical nuclear radius is femtometer, i.e. 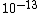 sm. Thus, the typical nuclear cross section sm. Thus, the typical nuclear cross section ^2\sim10^{-26} {sm}^2) . Actually, this is not a solution, but if you lose your way during exam, it might help:) And I found (C) exactly this way before using the Yosun's solution. . Actually, this is not a solution, but if you lose your way during exam, it might help:) And I found (C) exactly this way before using the Yosun's solution. |  |
|
|
Comments |
Fily
2011-03-18 09:06:10 | Of course answer above is correct,but one correction is required,(10E2/10E12)(1/10E20)(1/10E-4) will give 10E-26. |  | Imperate
2008-10-17 06:42:18 | It's obvious that the "useful area" (the area that will actually scatter if hit) is [latex] n \sigma A [/latex] were n is the number of target atoms per unit area, and A is the area (in some other GRE questions one has number density per volume and the thickness too but that's not the case here). The scattering probability is thus [latex] \frac{ n \sigma A}{A} =n \sigma[/latex]. Therefor if [latex] N_I [/latex] is the number of incident protons and [latex] N_S [/latex] is the number of scattered protons. One has [latex]N_S=n \sigma N_I [/latex] which is gives the total cross section as [latex] \sigma=\frac{N_S}{n N_I} [/latex]. Now to get differential cross section (per steradian) we just divide by the solid angle provided [latex] \sigma=\frac{N_S}{n N_I \Omega} [/latex]. Plug in the numbers.
Imperate
2008-10-17 06:45:21 |
oops....
It's obvious that the "useful area" (the area that will actually scatter if hit) is 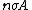 were n is the number of target atoms per unit area, and A is the area (in some other GRE questions one has number density per volume and the thickness too but that's not the case here). The scattering probability is thus were n is the number of target atoms per unit area, and A is the area (in some other GRE questions one has number density per volume and the thickness too but that's not the case here). The scattering probability is thus 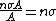 Therefore if Therefore if 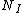 is the number of incident protons and is the number of incident protons and 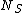 is the number of scattered protons. One has is the number of scattered protons. One has 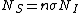 which is gives the total cross section as which is gives the total cross section as 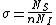 .Now to get differential cross section (per steradian) we just divide by the solid angle provided .Now to get differential cross section (per steradian) we just divide by the solid angle provided 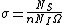 Plug in the numbers. Plug in the numbers.
|
|  | student2008
2008-10-16 14:29:27 | One can answer the question without solving it, recalling that the typical nuclear radius is femtometer, i.e. 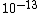 sm. Thus, the typical nuclear cross section sm. Thus, the typical nuclear cross section ^2\sim10^{-26} {sm}^2) . Actually, this is not a solution, but if you lose your way during exam, it might help:) And I found (C) exactly this way before using the Yosun's solution. . Actually, this is not a solution, but if you lose your way during exam, it might help:) And I found (C) exactly this way before using the Yosun's solution.
nyuko
2009-10-30 22:58:05 |
Sorry...I guess you have a typo, should be 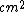 not not 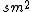 ? ?
by the way, I feel a little uncomfortable with your method because just a factor of 3 or 4 in length, after taking square, you would get an extra 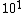 in the area. And for this problem, an order difference would lead to another answer. in the area. And for this problem, an order difference would lead to another answer.
What's more, those are charged particles (well, and not only coulomb interactions can take part; there are many others...). It is possible to have a cross section much different from the particle size...
|
|  | ric
2006-11-25 03:30:21 | I think that the solution should sound like this.
Call 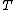 the number of scattered events (protons in this case) per second. We are given the "superficial" density of the target the number of scattered events (protons in this case) per second. We are given the "superficial" density of the target 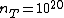 protons/ protons/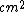 and the number of protons incident per second and the number of protons incident per second 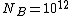 . Calling . Calling  the total cross section we have the total cross section we have
 T=N_B \,n_T\,\sigma T=N_B \,n_T\,\sigma . .
We are then given the value 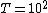 protons per second for a solid angle protons per second for a solid angle 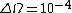 sterad. sterad.
Thus the differential cross section is
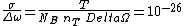 cm cm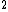 /sterad /sterad
|  | ric
2006-11-25 03:27:08 | I think that the solution should sound like this.
Call 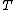 the number of scattered events (protons in this case) per second. We are given the "superficial" density of the target the number of scattered events (protons in this case) per second. We are given the "superficial" density of the target 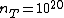 protons/ protons/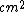 and the number of protons incident per second and the number of protons incident per second 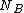 . Calling . Calling  the total cross section we have the total cross section we have
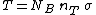 . .
We are then given the value 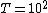 protons per second for a solid angle protons per second for a solid angle 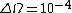 sterad. sterad.
Thus the differential cross section is
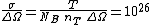 cm cm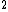 /sterad /sterad
|  | ric
2006-11-25 03:25:31 | I think that the solution should sound like this.
Call 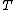 the number of scattered events (protons in this case) per second. We are given the "superficial" density of the target the number of scattered events (protons in this case) per second. We are given the "superficial" density of the target 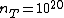 protons/ protons/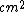 and the number of protons incident per second and the number of protons incident per second 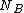 . Calling . Calling  the total cross section we have the total cross section we have
 T=N_B \,n_T\,\sigma T=N_B \,n_T\,\sigma . .
We are then given the value 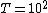 protons per second for a solid angle protons per second for a solid angle 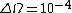 sterad. sterad.
Thus the differential cross section is
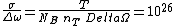 cm cm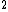 /sterad /sterad
|  | ric
2006-11-25 03:06:36 | |  | kevglynn
2006-10-17 19:35:32 | I hate to be a pain, but does anyone have a sound physics solution to this problem? I have found a couple of relations for the differential scattering cross section, but they haven't been very helpful.
kolahalb
2007-11-11 07:53:06 |
I do not intend to show ric's job is not good.But,this can be done by dimensional analysis and simple reasonings...
We must have cm^2/steradian.So,directly hit:
(1/(10^20))(1/(10^-4))=(10^-16) cm^2/steradian
Now,We must multiply the ratio between number of incident (I) and scattered (S) protons to (10^-16) cm^2/steradian.Otherwise the units will not match.The fraction may be (I/S) or,(S/I).We do not know.
If it is (I/S),note that the diameter of the scattering nucleus becomes rougly 10^-3 cm!!!
[As (pi*(r^2))~(10^-6)]
The other option is to multiply (10^-16) by (S/I) which preserves the units and gives a correct estimate of nulear dimension:
(10^-13) cm=(10^-15) m
|
flyboy621
2010-10-23 05:09:00 |
Looks like Ric has it right.
|
|  | Andresito
2006-03-30 12:22:52 | (1/10^20) is incorrect.
The correct ratio is (1/10^12)
grae313
2007-11-02 21:35:56 |
Yes, this typo should definitely be fixed! The answer should have a 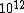 in the denominator, not two in the denominator, not two 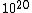 's 's
Thank you, Yosun
|
|  |
|
| Post A Comment! |
You are replying to:
I think that the solution should sound like this.
Call 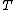 the number of scattered events (protons in this case) per second. We are given the "superficial" density of the target 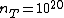 protons/ 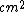 and the number of protons incident per second 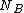 . Calling  the total cross section we have
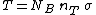 .
We are then given the value 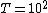 protons per second for a solid angle 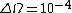 sterad.
Thus the differential cross section is
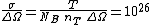 cm 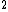 /sterad
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
