|
GR9277 #93
|
|
|
|
|
Alternate Solutions |
his dudeness
2010-09-05 15:55:11 | Yosun's method is clearly by far the best for this particular problem. However, if anyone is curious about how the relation in (E) is actually derived, here you go:
The acceleration can be split into radial and transverse components. Since gravity is the only force contributing to transverse acceleration, We have ) . To calculate . To calculate 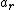 , we note that , we note that 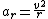 . From conservation of energy, we have . From conservation of energy, we have ) , so we get , so we get ) . .
All together now: ^2+4gsin(\theta)^2}) . A simple trig identity gets us the (E). . A simple trig identity gets us the (E). |  | jburkart
2007-11-02 00:23:15 | A real way to do the problem is as follows. Kinetic energy is 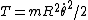 , where , where 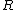 is the length of the string; potential is is the length of the string; potential is 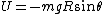 . Setting the Lagrangian to . Setting the Lagrangian to 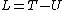 , Lagrange's equation is , Lagrange's equation is 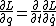 . In our case . In our case 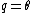 and we find and we find 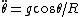 , which then yields , which then yields 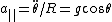 . But this is only the acceleration along the direction of motion; there is also a perpendicular centripetal acceleration given by . But this is only the acceleration along the direction of motion; there is also a perpendicular centripetal acceleration given by 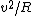 . To find . To find  we can invoke conservation of energy: we can invoke conservation of energy: 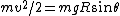 , so , so 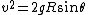 , so the centripetal acceleration is , so the centripetal acceleration is 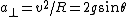 . .
Taking the norm of the the two acceleration components, we get 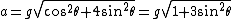 , answer (E). , answer (E).
A common mistake would be to omit the calculation of the centripetal acceleration, which would yield an incorrect answer of 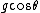 , which ETS kindly does not give as an option. , which ETS kindly does not give as an option. |  |
|
|
Comments |
his dudeness
2010-09-05 15:55:11 | Yosun's method is clearly by far the best for this particular problem. However, if anyone is curious about how the relation in (E) is actually derived, here you go:
The acceleration can be split into radial and transverse components. Since gravity is the only force contributing to transverse acceleration, We have ) . To calculate . To calculate 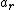 , we note that , we note that 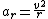 . From conservation of energy, we have . From conservation of energy, we have ) , so we get , so we get ) . .
All together now: ^2+4gsin(\theta)^2}) . A simple trig identity gets us the (E). . A simple trig identity gets us the (E).
physicsres.com
2014-11-15 12:55:37 |
good answer just a typo alert.
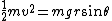
|
unurbat
2016-06-28 23:24:16 |
Where did the \"r\" disappear when you try to find radial acceleration?
|
|  | elzoido238
2008-11-06 11:02:47 | Answer choice C should be 2g sin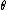 . . |  | Poop Loops
2008-10-25 20:22:52 | Oh Jesus, people, get all this nonsense away. Calculations on the GRE? That's suicide!
Here's how you think of it:
When 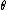 is is 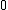 , the mass wants to go straight down, so a = g. , the mass wants to go straight down, so a = g.
That's it. Only E survives that.
But, if you had a different choice of answers, you can also think that acceleration is a maximum at 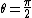 , because it also has centripetal acceleration, which adds to the gravitational force at that point. This obviously corresponds to sin, so there you go. , because it also has centripetal acceleration, which adds to the gravitational force at that point. This obviously corresponds to sin, so there you go.
ajkp2557
2009-11-03 13:57:32 |
"Calculations on the GRE? That's suicide!"
Best. Advice. Ever. The PGRE is entirely about test taking strategy. Yes, once you are in grad school it will be very important to know how to correctly work every problem, but spending four minutes on a problem on a test that only gives you 1.7 minutes per problem isn't a smart approach. You get the same credit for the answer, regardless of how you got it.
Work smarter, not harder. Best of luck!
|
|  | ayabepaula
2008-10-22 00:36:22 | time= zero
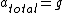
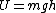
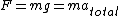
time
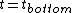
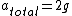
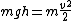
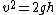
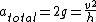
)
runcibleshaw
2015-08-16 06:54:34 |
I don\'t understand why the acceleration is 2g at the bottom. The total acceleration is the combination of g, which points down and the centripetal acceleration which points up, so it must be less than g total, right?
|
|  | wangjj0120
2008-10-08 12:42:19 | I am confused, why can't I use
=T=) force on string, so force on string, so 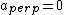 , and , and =m(l\ddot{\theta})=ma_{para}) , where , where 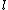 =length of string. From this, =length of string. From this, ) is correct, but is correct, but 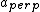 is wrong. Obviously the concept is incorrect here, but why? is wrong. Obviously the concept is incorrect here, but why?
iplayterran
2010-03-13 17:03:00 |
The tension force 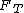 on the string is the sum of on the string is the sum of ) and the centripetal force and the centripetal force 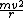 . If you use Newton's second law, . If you use Newton's second law,
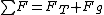
and decompose the forces into radial and angular components, you have
\hat{r} + (-mg\sin\theta)\hat{r} + (mg\cos\theta)\hat{\theta})
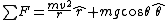
find velocity using conservation of energy, then find the magnitude of the above vector gives the correct answer E.
|
|  | jburkart
2007-11-02 00:23:15 | A real way to do the problem is as follows. Kinetic energy is 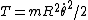 , where , where 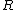 is the length of the string; potential is is the length of the string; potential is 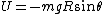 . Setting the Lagrangian to . Setting the Lagrangian to 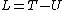 , Lagrange's equation is , Lagrange's equation is 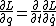 . In our case . In our case 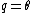 and we find and we find 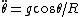 , which then yields , which then yields 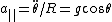 . But this is only the acceleration along the direction of motion; there is also a perpendicular centripetal acceleration given by . But this is only the acceleration along the direction of motion; there is also a perpendicular centripetal acceleration given by 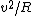 . To find . To find  we can invoke conservation of energy: we can invoke conservation of energy: 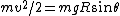 , so , so 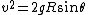 , so the centripetal acceleration is , so the centripetal acceleration is 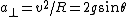 . .
Taking the norm of the the two acceleration components, we get 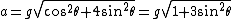 , answer (E). , answer (E).
A common mistake would be to omit the calculation of the centripetal acceleration, which would yield an incorrect answer of 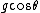 , which ETS kindly does not give as an option. , which ETS kindly does not give as an option.
kroner
2009-10-06 22:29:16 |
You don't need to do all that work to find the tangential acceleration. It's just the tangential component of gravity, which is 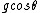 . .
|
|  | kb
2007-10-28 22:49:32 | is E is correct, can someone explain why
a(pi/2) = sqrt(3+1)g = 2g?
kb
2007-10-29 16:52:27 |
sorry, typo
"if E is correct, can someone explain why a(pi/2) = sqrt(3+1)g = 2g?"
and should go under "help!"
|
jburkart
2007-11-02 00:25:23 |
Because at that point the mass is experiencing a lot of g's! Try swinging in a swing sometime--you feel a lot of acceleration at the bottom.
|
evanb
2008-06-26 19:26:17 |
At the top, the energy is 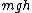 , and at the bottom it is , and at the bottom it is 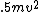 . .
This leaves us with 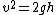 , and , and 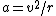 , but , but 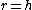 , so , so 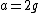 . .
|
|  | rmyers
2006-12-01 13:29:01 | The first four words should be edited out of this solution.
lambda
2007-10-21 22:13:29 |
I agree. This test can't be finished in the time allowed if one tries to apply "rigorous physics"!
|
ndubuisi
2011-11-05 01:52:04 |
But one must answer a quetn well,rather than apply tricks n fail
|
|  | Andresito
2006-03-30 12:05:12 | Thank you for the advice. :)
ayabepaula
2008-10-22 00:03:57 |
1)http://dev.physicslab.org/img/db0bf4f1-2f9b-428f-81a6-536588e8a7ce.gif
2)http://www.physics-lab.net/applets/simple-pendulum
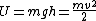
then
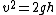
Gravitational acceleration:
********radial direction***************
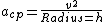
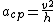
then
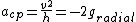 (negative sign --> (negative sign -->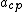 and and 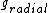 --> opposite direction. --> opposite direction.
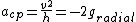 ( r-direction) ( r-direction)
)=2g(sin90)(sin\theta))
)
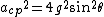
Gravitational acceleration
********tangential direction********
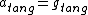 (t-direction) (t-direction)
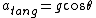
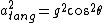
********total acceleration*********
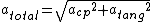
***********************************************
using
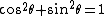
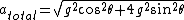
+ 4{g^2}sin{^2}\theta})
********
therefore:
The magnitude of the total acceleration of the mass as a function of the angle 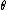 is: is:
********
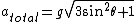
********
Paula Ayabe Pereira
|
|  |
|
| Post A Comment! |
You are replying to:
A real way to do the problem is as follows. Kinetic energy is 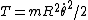 , where 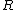 is the length of the string; potential is 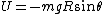 . Setting the Lagrangian to 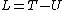 , Lagrange's equation is 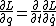 . In our case 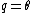 and we find 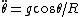 , which then yields 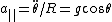 . But this is only the acceleration along the direction of motion; there is also a perpendicular centripetal acceleration given by 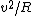 . To find  we can invoke conservation of energy: 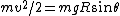 , so 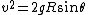 , so the centripetal acceleration is 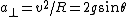 .
Taking the norm of the the two acceleration components, we get 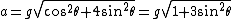 , answer (E).
A common mistake would be to omit the calculation of the centripetal acceleration, which would yield an incorrect answer of 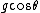 , which ETS kindly does not give as an option. |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
