|
GR9277 #89
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
NoPhysicist4
2017-03-23 14:53:40 | Do not mix infinite square well and harmonic potential as I did. In the first case, the numbering starts from 1, while the latter employs 0 as the initial state. Therefore the correct answer is E. |  | gravity
2010-11-05 01:50:43 | I spent five minutes trying to figure out why I keep getting the wrong answer here - then I finally realized that n=1 is an odd number (and not an even number like I kept trying to say it was) and that I'm an idiot. rnrnEven though it's the second energy level, the n is odd!
neon37
2010-11-12 07:57:18 |
Lol! If you get confused in the future. dont look at it that way. Infinite barrier at the origin means a node at origin. Which means odd only.
|
asdfuogh
2011-11-07 23:48:21 |
I think maybe he means that he saw odd as even and even as odd... which is what I did when I was rushing through these last ones :( damn.
|
|  | segfault
2009-09-06 09:23:40 | This doesn't make sense to me: assuming we do keep only the odd states, they themselves have a nonzero wavefunction at x<0. Even if you try to construct Psi=0 for x<0 using a superposition of states, then by symmetry of the odd states you'll also have Psi=0 for x>0. Halp!
kroner
2009-09-26 18:37:23 |
The eigenstates of this potential aren't literally the same as the odd ones for the harmonic oscillator. They're the same in the range x>0, which is enough to argue that their energy levels are the same.
|
dydtaylor
2015-10-16 16:01:23 |
They actually do go to 0 as x -> 0. The exponential terms go to 1, the odd Hermite polynomials go to 0 at 0 while the even Hermite polynomials have a constant in them and go to that constant.\r\n\r\nSee the hyperphysics article on the harmonic oscillator here: http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hosc5.html
|
|  | CaspianXI
2009-03-19 15:50:36 | Draw the wave functions for n = 0, 1, 2, 3, ... You'll quickly see that the wave functions for even values of n can't work, which leaves you with only odd values of n -- hence, (E).
This isn't a formal proof, but it's an easy way to grab the points for this problem and move on.
his dudeness
2010-09-05 14:52:10 |
also bear in mind that ETS usually begins indexing at n=0, as opposed to n=1, which most books tend to use. this convention interchanges even and odd functions -- I find that a quick sketch usually helps me out a lot.
|
|  | Furious
2007-10-29 22:00:30 | How is there a node in the middle of the well. This problem confused me a huge amount because it seems like there is not enough boundary conditions to solve, and that we should have some dampening sin function, since V gradually increases, rather than being infinite at a certain value.
Rune
2007-10-30 00:27:08 |
If you have the Griffiths QM book, Chapter 2 (pg 58 on mine) where there are graphs of of 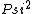 , which is the density function. The probability is zero at the center of the well for odd n (in other words there is a node, as the solution says here), meaning that if you put an infinite barrier there as the problem is doing, the odd states won't 'feel' the barrier, but the even n have a , which is the density function. The probability is zero at the center of the well for odd n (in other words there is a node, as the solution says here), meaning that if you put an infinite barrier there as the problem is doing, the odd states won't 'feel' the barrier, but the even n have a 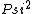 is not zero so those states 'feel' the barrier is not zero so those states 'feel' the barrier
|
neon37
2008-10-29 01:04:57 |
man the potential confused me for a while...i was trying to find the answer due to the potential. But it is the barrier that gives you the answer. Sines are odd functions and cosines are even functions. Cosine cant be since the wave function has to go to zero at x=0. So only odds are possible. Correct me if i'm wrong.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
