|
GR9277 #88
|
|
|
Problem
|
|
\prob{88}
A parallel-plate capacitor is connected to a battery. 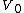 is the potential difference between the plates, is the potential difference between the plates,  is the charge on the positive plate, is the charge on the positive plate, 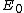 the magnitude of the electric field, and the magnitude of the electric field, and 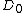 the magnitude of the displacement vector. The original vacuum between the plates is filled with a dielectric and then the battery is disconnected. If the corresponding electrical parameters for the final state of the capacitor are deonted by a subscript f, which of the following is true? the magnitude of the displacement vector. The original vacuum between the plates is filled with a dielectric and then the battery is disconnected. If the corresponding electrical parameters for the final state of the capacitor are deonted by a subscript f, which of the following is true?
-
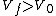
-
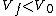
-

-

-
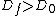
|
Electromagnetism }Capacitors }Capacitors
From the problem and the basic relation for capacitors  , one immediately deduces that the initial charge is , one immediately deduces that the initial charge is 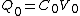 and the final charge is and the final charge is 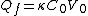 , and thus choice (C) is out. , and thus choice (C) is out.
The potential is constant  , and thus choices (A) and (B) are out. , and thus choices (A) and (B) are out.
The electric field for a parallel plate capacitor is given by 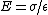 . Since . Since 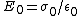 and and ) , the final field is the same as the initial field. (To wit: , the final field is the same as the initial field. (To wit: 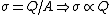 .) Thus, (D) is false. (Thanks to the user whose alias is "poop" for pointing this out.) .) Thus, (D) is false. (Thanks to the user whose alias is "poop" for pointing this out.)
From the definition of 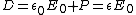 , one has , one has 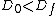 , since , since 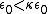 . Choice (E) is right. . Choice (E) is right.
|
|
|
Alternate Solutions |
Herminso
2009-09-22 16:03:08 | The first thing to put clear here is that the potential difference between the plates of a capacitor is maintained by the cattery while the dielectric is inserted. When the battery is disconnected, the potential difference on the capacitor remains constant  , since there is no way to discharging. Thus at first (A) and (B) are eliminated. , since there is no way to discharging. Thus at first (A) and (B) are eliminated.
Now, we know that the effect of the dielectric between the plates of the capacitor is to increase its capacity to accumulate energy, i.e, increase its capacitance, then 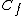 > > and and 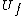 > >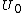 . Note also that if . Note also that if 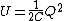  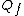 > >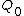 . The effect of the dielectric in this case is to increase the charge in the plates.Then (C) is out. . The effect of the dielectric in this case is to increase the charge in the plates.Then (C) is out.
By other hand, since ther is not free charge inside the region between the plates, hold the Poisson equation 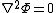  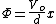 , so , so 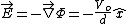 where where  is the separation between the plates and is the separation between the plates and 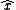 is along de direction orthogonal to both plates betwen them. Thus the final field is the same as the initial field, since is along de direction orthogonal to both plates betwen them. Thus the final field is the same as the initial field, since   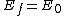 . Thus (D) is also eliminated. . Thus (D) is also eliminated.
In addition since the electric field inside of the plates according to Gauss law is 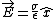 and and 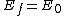 as we concluded, then as we concluded, then 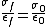 or or 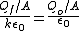  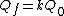 and and 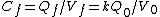  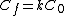 . .
Finallywe can use 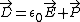 to see that (E) is true. In the beginning, there is not polarization, thus to see that (E) is true. In the beginning, there is not polarization, thus 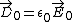 , but after the dielectric is inserted , but after the dielectric is inserted 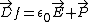   > >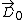 . .
Note that if the battery was disconnected before the insertion of the dielectric block, it's a different problem that works in other way. See explanation of  on on  's Comment. 's Comment. |  |
|
|
Comments |
jcsoldier11
2010-11-10 03:33:58 | I eliminated all answers but (E) very quickly and qualitatively.
Since the dielectric is inserted while the capacitor is still attached to the battery, the potential across it is the same meaning the capacitance changes due to a change in the charge from C = V/Q. This eliminates (A) , (B) and (C).
(D) can be eliminated because the voltage difference and the distance between the plates is not changing, so simply using V = E * d the electric field must be the same. Even if it DID change, it would be decreased by a factor of the dielectric constant, so (D) would still not be true.
(E) is the only answer left in a matter of seconds and only basic formulas. =) |  | Herminso
2009-09-22 16:03:08 | The first thing to put clear here is that the potential difference between the plates of a capacitor is maintained by the cattery while the dielectric is inserted. When the battery is disconnected, the potential difference on the capacitor remains constant  , since there is no way to discharging. Thus at first (A) and (B) are eliminated. , since there is no way to discharging. Thus at first (A) and (B) are eliminated.
Now, we know that the effect of the dielectric between the plates of the capacitor is to increase its capacity to accumulate energy, i.e, increase its capacitance, then 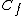 > > and and 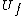 > >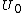 . Note also that if . Note also that if 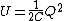  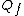 > >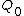 . The effect of the dielectric in this case is to increase the charge in the plates.Then (C) is out. . The effect of the dielectric in this case is to increase the charge in the plates.Then (C) is out.
By other hand, since ther is not free charge inside the region between the plates, hold the Poisson equation 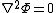  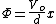 , so , so 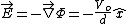 where where  is the separation between the plates and is the separation between the plates and 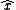 is along de direction orthogonal to both plates betwen them. Thus the final field is the same as the initial field, since is along de direction orthogonal to both plates betwen them. Thus the final field is the same as the initial field, since   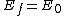 . Thus (D) is also eliminated. . Thus (D) is also eliminated.
In addition since the electric field inside of the plates according to Gauss law is 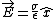 and and 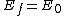 as we concluded, then as we concluded, then 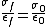 or or 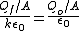  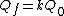 and and 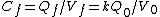  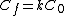 . .
Finallywe can use 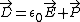 to see that (E) is true. In the beginning, there is not polarization, thus to see that (E) is true. In the beginning, there is not polarization, thus 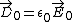 , but after the dielectric is inserted , but after the dielectric is inserted 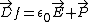   > >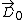 . .
Note that if the battery was disconnected before the insertion of the dielectric block, it's a different problem that works in other way. See explanation of  on on  's Comment. 's Comment. |  | vsravani
2008-11-01 05:32:00 | Am totally confused with the answers. According to a text book that I have read, it says -
"If the battery is removed after fully charging the capacitor, the effect of dielectric is to reduce the potential difference between the plates, and to maintain charge. Charge is maintained because, there is no place for the capacitor to discharge."
and
"If potential difference between the plates of a capacitor is maintained by the battery, the effect of dielectric is to increase the charge in the plate"
From this it turns out to that both B and C are correct. Can anybody help me as to what is wrong.
a19grey2
2008-11-02 14:53:23 |
I think you are mis-reading the question. Your first quote applies ONLY if the battery is disconnected before the insertion of the dielectric block. In the problem this is not the case. The dielectric is inserted while the battery is still connected.
Thus, your second quote IS accurate and the charge on the plates does increase. If the charge on the plates increases, then C is false. Also, since the "potential difference is maintained by the battery" there is no change in the potential and thus A & B are both false.
|
|  | Jeremy
2007-11-03 14:21:17 | I think the easiest way to eliminate choice (D) is to use, as johnstaples already has, 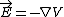 . This immediately shows that . This immediately shows that  is unchanged without the need to consider charges. As a side note, this equation, without even using is unchanged without the need to consider charges. As a side note, this equation, without even using 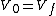 , eliminates choices (A) and (D) because each implies the other (assuming fixed capacitor plate spacing and only one correct answer choice). , eliminates choices (A) and (D) because each implies the other (assuming fixed capacitor plate spacing and only one correct answer choice). |  | ec2250
2007-08-31 16:55:59 | I'm confused. According to griffiths 3rd edition, page 183 example 4.6, he says that when a parallel-plate capacitor is filled with insulating material, it will reduce  which will also reduce the potential difference. And if E is the correct answer, wouldn't that mean that which will also reduce the potential difference. And if E is the correct answer, wouldn't that mean that  final is not equal to final is not equal to  intial because D = e(0) intial because D = e(0)  + P. So D initial is just e(0) + P. So D initial is just e(0)  because there is no dielectric. D final is e(0) because there is no dielectric. D final is e(0)  + P because of the dielectric. Then + P because of the dielectric. Then  final would be less by subtracting P from D. final would be less by subtracting P from D.
johnstaples
2007-09-19 11:00:10 |
Hi,rnI haven't checked your citation of Griffiths, but I'm assuming that in his example the capacitor is not connected to a battery while the dielectric is being inserted. The presence of the battery forces the potential difference across the capacitor to remain constant (Vo = Vf) and thus the electric field is also held constant ( = - grad V). Without the battery, the charge on the capacitor plates would have to remain constant, and so changing the capacitance (ie, inserting a dielectric) would necessarily change the potential difference across the plates (and hence the electric field). Furthermore, because the polarization vector is initially 0 before inserting the dielectric, you have Do = = - grad V). Without the battery, the charge on the capacitor plates would have to remain constant, and so changing the capacitance (ie, inserting a dielectric) would necessarily change the potential difference across the plates (and hence the electric field). Furthermore, because the polarization vector is initially 0 before inserting the dielectric, you have Do = 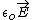 + + 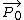 = = 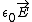 and after inserting you have Df = and after inserting you have Df = 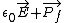 = = 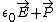 , which are not equal. , which are not equal.
|
|  | poop
2005-11-23 15:40:51 | Since sigma is proportional to Q, sigma_f is not equal to sigma_0 -- after taking that into account, I think it turns out E_f is equal to E_0.
yosun
2005-11-23 15:51:35 |
to user alias poop: thanks for the correction; i've updated the solution accordingly.
|
dumbguy
2007-10-19 08:46:59 |
Actually E final will be less then E initial. Thats casue Ef=E0/k.
|
natec
2013-09-03 13:05:54 |
the equation 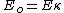 assumes the charge on the plates is kept constant, so in this case it is not necessarily true that E final will be less than E initial. I don't have proof, but I think that it is true that E final = E initial like yosun says in the solution. assumes the charge on the plates is kept constant, so in this case it is not necessarily true that E final will be less than E initial. I don't have proof, but I think that it is true that E final = E initial like yosun says in the solution.
|
natec
2013-09-03 13:12:37 |
after re-reading the solution, I found the proof... E final does indeed equal E initial
|
|  | mrk00k
2005-11-11 22:27:41 | |  | angryJ
2005-11-11 17:41:38 | Wow, this is fucking WRONG asswads. Read a book!
erc
2005-11-11 18:40:14 |
If you know the correct answer, why not help out the community by posting it, instead of being obscene and insulting?
Yosun has worked wonders to get this site up and available in the last few days, and I think she should be heaped with praise. It has proved an invaluable aid to me, and if you cannot be grateful for what is here, and are not willing to help out with improvements, you can always just move along.
Thank you Yosun, and all the other commenters who have put useful remarks up. And GOOD LUCK to all those taking the test tomorrow (like me)!
|
yosun
2005-11-11 20:29:47 |
erc: good luck to you too.
angryJ: what the f* is wrong with this?
|
mrk00k
2005-11-11 22:29:17 |
uhh, oops, what I meant was:
you have a small typo, you say for (D) the final field is larger, but i think you mean smaller, but uhh, its just a typo, relax angryJ
|
yosun
2005-11-11 22:52:35 |
mrk00k: thanks for the typo-alert; it has been corrected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
