|
GR9277 #87
|
|
|
Problem
|
|
\prob{87}
A particle of mass M moves in a circular orbit of radius r around a fixed point under the influence of an attractive force 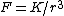 , where K is a constant. If the potential energy of the particle is zero at an infinite distance from the force center, the total energy of the particle in the circular orbit is , where K is a constant. If the potential energy of the particle is zero at an infinite distance from the force center, the total energy of the particle in the circular orbit is
-
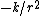
-
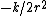
- 0
-
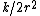
-
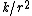
|
Mechanics }Conservation of Energy }Conservation of Energy
Do not immediately try applying the Virial Theorem to this one. Instead, consider conservation of energy. Coming in from far away, the particle has 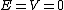 the total energy equal to the potential energy equal to 0. the total energy equal to the potential energy equal to 0.
Alternatively, one has, for a circular orbit, the equality between centripetal force and the attractive force, 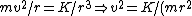) . .
Thus, the kinetic energy is just 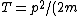 = K/(2r^2)) . .
Since 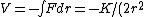) , where the extra negative sign for the potential energy is due to an attractive potential. , where the extra negative sign for the potential energy is due to an attractive potential.
Thus, the total energy 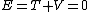 , which is choice (C). , which is choice (C).
(Alternate solution is due to user crichigno.) |
|
|
Alternate Solutions |
marching_band_to_nowhere
2019-09-02 22:19:21 | Circular orbits must occur at minimums of the potential energy curve. Since V is proportional to 1/r^3, the only minimum for r>0 is when E -> 0, so the only circular orbit has E = 0. |  | crichigno
2005-11-11 13:12:45 | I think a correct solution would be the following:
Since the orbit is circular, the centrifugal force and the attractive force should be balanced, hence
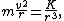
or equivalently
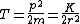
, but this is just minus the potential energy due to the force F, since
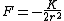
Finally
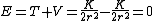 |  |
|
|
Comments |
marching_band_to_nowhere
2019-09-02 22:19:21 | Circular orbits must occur at minimums of the potential energy curve. Since V is proportional to 1/r^3, the only minimum for r>0 is when E -> 0, so the only circular orbit has E = 0.
marching_band_to_nowhere
2019-09-02 22:20:26 |
Whoops, F is proportional to 1/r^3, so the potential is actually proportional to 1/r^2. Argument still works, however.
|
|  | socolenco
2014-08-13 13:38:58 | I think we should use here the Principle of Work and Energy: Given that a particle undergoes a displacement under the influence of a force F, the work done by F equals the change in kinetic energy of the particle. The principle may be applied to a system of particles if each particle is considered separately:
_{1-2} = \left( KE\right)_{2} -\left( KE\right)_{1})
Kinetic Energy and Newton's Law:
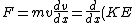) , where KE is a function of x. , where KE is a function of x.
At an infinite distance from the force center the particle had supposedly only the kinetic energy 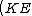_{1}) as we know for sure that it had zero potential energy. And this initial kinetic energy as we know for sure that it had zero potential energy. And this initial kinetic energy 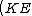_{1}) is its total energy: is its total energy:
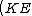_{1} = \left( KE\right)_{2} - \left( W\right)_{1-2} = Total Energy)
The final kinetic energy 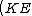_{2}) is obtained from the above Kinetic Energy and Newton's Law: is obtained from the above Kinetic Energy and Newton's Law:
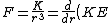_{2} \Rightarrow \left( KE\right)_{2} = -\frac{K}{2r^2})
The work done on the particle from infinity to r is:
_{1-2} =\int_\infty^rFdr=\int_\infty^r\frac{K}{r^3}=-\frac{K}{2r^2})
The total energy is then obtained:
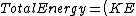_{1} = \left( KE\right)_{2} - \left( W\right)_{1-2}=-\frac{K}{2r^2}-(-\frac{K}{2r^2})=-\frac{K}{2r^2}+\frac{K}{2r^2}=0)
This tells us that the particle of mass M had not only zero potential energy, but also zero initial kinetic energy.
|  | packinski
2011-11-07 11:48:53 | Doesn't the Bertrand theorem say that the only potentials which give rise to stable closed orbits are proportional do ~ 1/r and r^2? Then how is it possible that a particle is moving in a circular orbit according to this law of force?
Nezumi
2012-01-18 09:05:06 |
My first guess would be that this orbit, while circular, is not stable.
|
Nezumi
2012-01-18 09:05:44 |
My first guess would be that this orbit, while circular, is not stable.
|
Nezumi
2012-01-18 09:05:44 |
My first guess would be that this orbit, while circular, is not stable.
|
MonaJalilvand
2015-10-21 07:15:34 |
I think any potential shape, which has a minimum, can have circular stable orbits. Since the derivative of radius is zero and it\'s a minimum point. So it is stable. But the existence of elliptical orbits is not trivial.
|
|  | skeptic
2010-11-11 21:58:26 | I wonder why this is not as simple as:
The energy was zero at infinity, no energy was lost, all kinetic came from potential, we're done, energy was conserved, it is still zero.
I suppose I am making a (hidden) statement that the force is conservative, but I think it is. The curl is clearly zero (it is pure divergence), and I think -grad of (K/2*r*r) potential will give us the Force.
(If you are uncomfortable doing curl in spherical coords, just recall that curl takes derivatives wrt the other cords, and this is a purely radial force, so the azimuthal and angular derivatives are zero. But a picture for me wins the day. This is just a sink in a higher dimension).
Anyone?
And good physics to all for Saturday. I don't mind saying I'm scared!
And thank you Yosun!
faith
2010-11-12 04:12:10 |
gawd it took me quite sometime just to figure out the signs!!! dont u just hate it?!! yea good physics on Sat! i'm taking it too~~ i'm freak out! the worst part is knowing.. i just had 3 years of physics course and boy there's so much iv not known b4.. looks like its all up to physics intuition. to all that shares my position, may ur intuition be clear and calm!
|
gear3
2013-10-11 01:50:21 |
According to your deduction, if we substitute f=k/r^3 with the normal gravititional force that is f=k/r^2, we will get the same result E=0. So your reasoning is wrong.
|
|  | skeptic
2010-11-11 21:36:47 | I think it is SO important to understand where - (and +) signs come from. Of course our test charges are always + positive (sources).
A sink has a negative potential and an attractive force. It must "be a hole" because it is a minimum and the second derivative is +. Test charges “fall into” it. They may get trapped and we may have SHO.
A source has a positive potential and a repulsive force. It must "be a hill" because it is a maximum and the second derivative is -. Test charges “run away” from it.
F=-gradU (Energy sinks have attractive force & Energy sources have repulsive force) (1)
E=-gradV (Potential sinks have attractive field & Potential sources have repulsive field) (2)
and we get (1) by dropping the (+) test charge into (2).
divE=ρ=-divgradV (here we have a second derivative, negative for a maximum or source)
For ρ +, a source, it is a potential hill, which has negative second derivative. It automatically gives us a positive E (or F). To get a positive E (or F) from the the second derivative of a potential hill, we need the -.
For ρ –, a sink, it is a potential hole, which has positive second derivative. It automatically gives us a negative E (or F). To get a negative field (or force) from the second derivative of a potential well, we need the -.
Of course, for electrons, hills become holes and holes become hills, or better, electrons “live on the other side”, instead of skiing the outside of the hill they fall underground to the top, but the math is unchanged, except that electrons can do SHO in "the top" of electric sources! |  | kroner
2009-09-26 18:23:49 | Notice the conspicuous 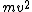 term in the equation term in the equation 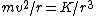 . Immediately . Immediately 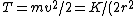) without any detour through momentum. without any detour through momentum. |  | CaspianXI
2009-03-19 15:39:27 | This is a tricky problem because they've given F (i.e., the magnitude of 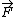 ), but you need to look carefully in order to realize that ), but you need to look carefully in order to realize that 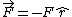 . If you're rushing, you might not realize this and loose credit for this problem. . If you're rushing, you might not realize this and loose credit for this problem.
Because potential energy is a funny thing, here's what I like to do. They've given that the potential energy is zero at r=infinity, and you know intuitively that the potential energy should increase the particle moves away from whatever source causes this attraction. If you have a sign error and get 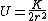 , with this simple check, you'll be able to easily realize your mistake and say, "Whoops! I guess it should be , with this simple check, you'll be able to easily realize your mistake and say, "Whoops! I guess it should be 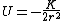 !" !"
NAThompson
2011-09-24 01:00:14 |
Ah thanks! That's exactly where I was getting confused on this problem!
|
|  | 94709
2007-10-21 16:36:05 | Why not applying Virial Theorem??? It works easily.
In the followings, time averaged kinetic and potential energies are expressed as 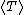 and and 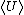 respectively. respectively.
Since it's circular orbit, 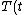=\langle T \rangle ) and and 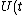=\langle U\rangle ) at all time. Given the force field, at all time. Given the force field, 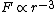 , we know that , we know that 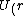\propto r^{-2} ) . .
Virial Theorem for 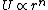 states; states;
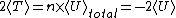
Therefore, 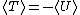 , and hence, , and hence, 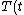=-U(t)) at all time. This concludes at all time. This concludes 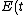=T(t)+U(t)=0) . .
gliese876d
2008-10-09 12:32:23 |
I think the reason the solution says not to use the Virial Theorem is that if you just blindly take the derivative of F in this case to obtain U as porportional to 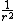 , then apply the Virial Theorem as many of us (myself included) have the Virial Theorem memorized: = 1/2 or -2 = , as is the case when dealing with a force proportional to , then apply the Virial Theorem as many of us (myself included) have the Virial Theorem memorized: = 1/2 or -2 = , as is the case when dealing with a force proportional to 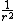 , but not the case for a force proportional to , but not the case for a force proportional to 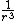 then you get choice B as an answer. This is an easy pitfall to fall into. Thus if you, like me, did not realize the caveat in the Virial Theorem that there is an N in front of (because we are used to that N simply equalling 1), then ETS has already set the trap for you to fall into by supplying the answer you would have gotten by misapplying the Virial Theorem. then you get choice B as an answer. This is an easy pitfall to fall into. Thus if you, like me, did not realize the caveat in the Virial Theorem that there is an N in front of (because we are used to that N simply equalling 1), then ETS has already set the trap for you to fall into by supplying the answer you would have gotten by misapplying the Virial Theorem.
|
|  | Mexicana
2007-10-04 18:38:41 | I agree with user georgi... The integral of Fdr doesnt give a a negative potential, so why should you interpret the constant 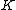 as being positive?? In the problem actually doesn't even specify whether as being positive?? In the problem actually doesn't even specify whether 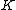 is positive or not, so in a way this is a pitfall of the ETS people putting ambiguous problems!!! arghhh is positive or not, so in a way this is a pitfall of the ETS people putting ambiguous problems!!! arghhh
apr2010
2010-04-08 13:00:29 |
I get a -1/2 out of the integral which makes the minus in front of it useless, but that is how u do it. I am not sure how to interpret this, one have to assume that k is smaller 0, I am fine with that.
|
|  | georgi
2007-08-27 00:20:40 | uhm, the negative integral of Fdr is positive right? then wouldn't you get T+V not being zero?
Mexicana
2007-10-04 18:39:21 |
I agree with user georgi... The integral of Fdr doesnt give a a negative potential, so why should you interpret the constant as being positive?? In the problem actually doesn't even specify whether is positive or not, so in a way this is a pitfall of the ETS people putting ambiguous problems!!! arghhh
|
Jeremy
2007-11-03 13:45:27 |
First off, notice that the problem gives only the magnitude of 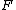 . It turns out the sign of . It turns out the sign of 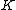 doesn't matter, but I agree it is confusing at first. In vector form, doesn't matter, but I agree it is confusing at first. In vector form, 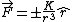 , with the plus if , with the plus if 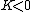 , and the minus if , and the minus if 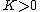 . Summing the forces, . Summing the forces, 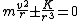 , or , or 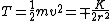 . (Remember that the top sign corresponds to . (Remember that the top sign corresponds to 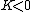 and the bottom sign is for and the bottom sign is for 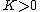 , so , so 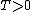 in both cases.) With the same sign conventions, in both cases.) With the same sign conventions, 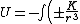 dr= \pm \frac{K}{2 r^{2}}+constant) . However, the problem states that . However, the problem states that =0) , so the constant of integration is zero. Finally, , so the constant of integration is zero. Finally, 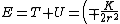+\left( \pm \frac{K}{2 r^{2}} \right)=0) . Notice that the official solution has used . Notice that the official solution has used 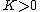 , and the comment "the extra negative sign for the potential energy is due to an attractive potential" means "we're using , and the comment "the extra negative sign for the potential energy is due to an attractive potential" means "we're using 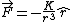 ." ."
|
|  | Andresito
2006-03-29 21:04:00 | I think this problem is excellent.
Note that a particle which moves around a fixed point (presumably of large density) has no net energy.
The system has kinetic energy and also posseses potential energy but happens to have them equal in magnitude and opposite in sign.
Probably this zero net energy was helpful on deriving early models of the atom but once there is charge associated there will be radiation.
oliTUTilo
2012-11-04 17:16:05 |
To be clear, it is not true in general that a system of a particle in circular orbit due to a central potential has zero total energy, or even a constant energy over different radial orbits. In general, such a particle's kinetic energy is 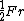 where where 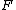 is the central force, but the potential energy where the central force is proportional to is the central force, but the potential energy where the central force is proportional to 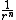 for for  > >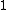 is is 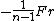 so that the total energy is so that the total energy is ) , and that's assuming we let the potential at infinity go to zero (otherwise you tack on a constant). , and that's assuming we let the potential at infinity go to zero (otherwise you tack on a constant).
|
|  | crichigno
2005-11-11 13:12:45 | I think a correct solution would be the following:
Since the orbit is circular, the centrifugal force and the attractive force should be balanced, hence
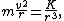
or equivalently
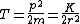
, but this is just minus the potential energy due to the force F, since
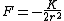
Finally
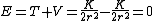
crichigno
2005-11-11 13:16:54 |
Sorry, I meant:
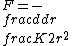
|
yosun
2005-11-11 13:51:32 |
crichigno: thanks for your alternate solution; i've taken your hint for the solution and posted it up.
|
Mexicana
2007-10-04 18:42:38 |
First of all you made a typo mistake and misplaced an 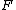 instead of a instead of a 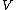 for the potential on your third equation. for the potential on your third equation.
The second issue is that I feel everyone is not justifying properly the imposition of a minus sign to the potential- the constant 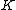 isn't defined as positive or negative in the problem! This is really a severe typo/ambiguity from the ETS people!!! isn't defined as positive or negative in the problem! This is really a severe typo/ambiguity from the ETS people!!!
|
out_2physics
2009-09-27 16:42:23 |
Mexicana, the reason the potential energy is negative is because the question stated that the force is an attractive force. For reason i don't know, in physics an attractive force is indicated with a negative sign.
|
|  |
|
| Post A Comment! |
You are replying to:
I think it is SO important to understand where - (and +) signs come from. Of course our test charges are always + positive (sources).
A sink has a negative potential and an attractive force. It must "be a hole" because it is a minimum and the second derivative is +. Test charges “fall into” it. They may get trapped and we may have SHO.
A source has a positive potential and a repulsive force. It must "be a hill" because it is a maximum and the second derivative is -. Test charges “run away” from it.
F=-gradU (Energy sinks have attractive force & Energy sources have repulsive force) (1)
E=-gradV (Potential sinks have attractive field & Potential sources have repulsive field) (2)
and we get (1) by dropping the (+) test charge into (2).
divE=ρ=-divgradV (here we have a second derivative, negative for a maximum or source)
For ρ +, a source, it is a potential hill, which has negative second derivative. It automatically gives us a positive E (or F). To get a positive E (or F) from the the second derivative of a potential hill, we need the -.
For ρ –, a sink, it is a potential hole, which has positive second derivative. It automatically gives us a negative E (or F). To get a negative field (or force) from the second derivative of a potential well, we need the -.
Of course, for electrons, hills become holes and holes become hills, or better, electrons “live on the other side”, instead of skiing the outside of the hill they fall underground to the top, but the math is unchanged, except that electrons can do SHO in "the top" of electric sources!
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
