|
GR9277 #83
|
|
|
|
|
Alternate Solutions |
cjohnson415
2013-08-19 01:40:11 | Here's an alternative solution that skips the trig altogether:
Due to small  , we can consider each as a simple pendulum, a special case of the simple harmonic oscillator: , we can consider each as a simple pendulum, a special case of the simple harmonic oscillator:
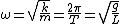
Thus 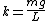 , which is the restoring force constant ( , which is the restoring force constant (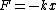 ), so: ), so:
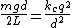
The rest is the same algebra, just a different/potentially quicker/potentially prettier way to arrive at the force balance. |  | neo55378008
2012-08-18 12:27:15 | Dimensional analysis helps!
Since 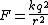 is in N, is in N, 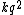 will have units of will have units of 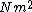
Mg has units of N
so 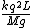 will have units of will have units of 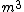
This leaves only A and B. Knowing that solving for  will give half of d, take the solution with an extra 2 in it! (A) will give half of d, take the solution with an extra 2 in it! (A) |  | redmomatt
2011-11-06 08:25:21 | Heres another take without the trig functions...
Since  is small, we can remove all of the trig functions. Thus, we just need to equate the outward Coulomb force is small, we can remove all of the trig functions. Thus, we just need to equate the outward Coulomb force 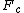 to the force of gravity along the horizontal to the force of gravity along the horizontal 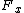 . .
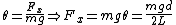 , since , since 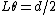 . .
Hence,
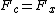  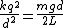  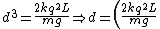^{1/3}) , which is (B) . , which is (B) . |  | Andresito
2006-03-29 14:56:46 | It is a bit faster to equate F(electric) = T*Sin(theta), m*g = T*Cos(theta) and divide them. Tan(theta) ~ theta |  |
|
|
Comments |
astropolo
2014-07-29 11:55:16 | I have a quick question about the small angle approximations. Why can you approximate that Cos~1 while you use the geometry for Sin rather than saying sin~theta?
JoshWasHere
2014-08-20 08:20:22 |
When you expand cosine and sine, you see that the first two terms in the cosine and sine expansion are cos = 1 - = 1 - 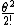 and sin and sin = =  - -  . Because of the small angle, we select only the first order terms, and drop all higher order terms (with the condition that . Because of the small angle, we select only the first order terms, and drop all higher order terms (with the condition that  < 5 degrees). < 5 degrees).
|
|  | cjohnson415
2013-08-19 01:40:11 | Here's an alternative solution that skips the trig altogether:
Due to small  , we can consider each as a simple pendulum, a special case of the simple harmonic oscillator: , we can consider each as a simple pendulum, a special case of the simple harmonic oscillator:
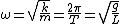
Thus 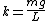 , which is the restoring force constant ( , which is the restoring force constant (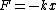 ), so: ), so:
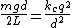
The rest is the same algebra, just a different/potentially quicker/potentially prettier way to arrive at the force balance. |  | greatspirits
2012-11-02 15:49:28 | Energy conservation anyone? The change in gravitational potential energy should equate to potential between the charges. So... 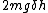 should equate to... hmmm well I usually prefer the energy method but the force way seems to be more effecient here. should equate to... hmmm well I usually prefer the energy method but the force way seems to be more effecient here. |  | neo55378008
2012-08-18 12:27:15 | Dimensional analysis helps!
Since 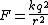 is in N, is in N, 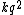 will have units of will have units of 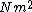
Mg has units of N
so 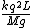 will have units of will have units of 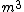
This leaves only A and B. Knowing that solving for  will give half of d, take the solution with an extra 2 in it! (A) will give half of d, take the solution with an extra 2 in it! (A)
henryb
2016-09-12 18:14:40 |
thx a lot. this is the simplest solution
|
|  | redmomatt
2011-11-06 08:25:21 | Heres another take without the trig functions...
Since  is small, we can remove all of the trig functions. Thus, we just need to equate the outward Coulomb force is small, we can remove all of the trig functions. Thus, we just need to equate the outward Coulomb force 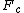 to the force of gravity along the horizontal to the force of gravity along the horizontal 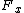 . .
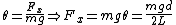 , since , since 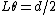 . .
Hence,
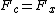  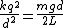  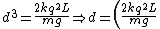^{1/3}) , which is (B) . , which is (B) . |  | Dodobird
2010-11-12 11:57:31 | tan(theta) = d/2L
tan(theta) = kq*q/d*d*MG
d/2L = kq*q/d*d*MG
gives answer A. |  | FortranMan
2008-10-03 14:02:49 | Also note because theta is so small here, we can approximate the vector component of the gravity that's NOT inducing tension to be d/2. |  | JAS
2007-11-01 09:20:45 | It seems easier to equate torques around the pivot point, where the torque on the right mass due to the repulsive electric force isrnrn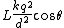 counterclockwisernrnand the torque on the right mass due to its weight is:rnrn counterclockwisernrnand the torque on the right mass due to its weight is:rnrn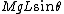 clockwisernrn clockwisernrn and and 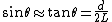 rnrnFrom this, choice A follows. rnrnFrom this, choice A follows. |  | relain
2007-10-23 19:21:51 | typo in the question, option D should be a square not a cube root. It's currently identical to option B. |  | Andresito
2006-03-29 14:56:46 | It is a bit faster to equate F(electric) = T*Sin(theta), m*g = T*Cos(theta) and divide them. Tan(theta) ~ theta |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
