|
GR9277 #71
|
|
|
|
|
Alternate Solutions |
Herminso
2009-09-22 19:12:05 | For  , all of the systems are in the lowest energy state (minimum entropy), so the only choice is (B). , all of the systems are in the lowest energy state (minimum entropy), so the only choice is (B). |  | ramparts
2009-08-15 20:35:32 | All the solutions are so complicated! :( Here's a way for us stat mech idiots using boundary conditions:
For 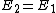 (or epsilon=0), this should go to (or epsilon=0), this should go to 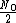 . That leaves B and E. (and technically A but that's clearly wrong :) ). . That leaves B and E. (and technically A but that's clearly wrong :) ).
Now E_2 > E_1 so the answer has to be less than 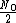 for positive epsilon. That leaves B. for positive epsilon. That leaves B. |  | moonrazor
2006-03-27 13:37:23 | (GR9277-71) Alternate Solution with less assumptions:
Using P(E) = (1/Z)exp[-E/kT] we have
P(E_1) = exp[-E_1/kT] / (exp[-E_1/kT] + exp[-E_2/kT])
= 1 / (1 + exp[-(E_1-E_2)/kT])
= 1 / (1 + exp[-\epsilon /kT])
LaTeX
\begin{eqnarray*}
P(E_{1}) &=& \frac{e^{-E_{1}/kT}}{e^{-E_{1}/kT} + e^{-E_{2}/kT}}\\
&=& \frac{1}{1 + e^{-(E_{2}-E_{1})/kT}}\\
&=& \frac{1}{1 + e^{-\epsilon/kT}}
\end{eqnarray*}
radicaltyro
2006-10-31 14:05:37 |
Hi moonrazor. Wrap your latex in single dollar signs.
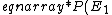 &=& \frac{e^{-E_{1}/kT}}{e^{-E_{1}/kT} + e^{-E_{2}/kT}}\\&=& \frac{1}{1 + e^{-(E_{2}-E_{1})/kT}}\\&=& \frac{1}{1 + e^{-\epsilon/kT}} \end{eqnarray*})
|
|  |
|
|
Comments |
ernest21
2019-09-30 04:59:09 | Cool! I\'ll surely be coming back for the next posts from you. You\'re an incredibly engaging writer that I can freely recommend this article to my college students. clash royale best decks |  | ernest21
2019-09-30 04:57:11 | Cool! I\'ll surely be coming back for the next posts from you. You\'re an incredibly engaging writer that I can freely recommend this article to my college students. clash royale best decks |  | ernest21
2019-09-30 04:55:51 | Cool! I\'ll surely be coming back for the next posts from you. You\'re an incredibly engaging writer that I can freely recommend this article to my college students. clash royale best decks |  | juliano lorenso
2014-10-09 17:14:43 | This is how I see it ..
1) As T--> 0, energy distribution for fermions must reduce to 1/2. So, in our case, it has to be proportional to N0/2.
2) E1 is proportional to +epsilon and E2 is proportional to -epsilon
Since we were asked to find the average number of subsystems in the state of energy E1, we can safely eliminate D and E because they have -epsilon and we want +epsilon
A is correct if we're talking about classical systems in normal conditions, so we eliminate it
B is incorrect because as T-->0, we get N0 and that's nonsense
So the correct answer is (C) .. If we apply T-->0 we get N0/2
Voila!!!! |  | Herminso
2009-09-22 19:12:05 | For  , all of the systems are in the lowest energy state (minimum entropy), so the only choice is (B). , all of the systems are in the lowest energy state (minimum entropy), so the only choice is (B). |  | ramparts
2009-08-15 20:35:32 | All the solutions are so complicated! :( Here's a way for us stat mech idiots using boundary conditions:
For 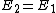 (or epsilon=0), this should go to (or epsilon=0), this should go to 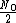 . That leaves B and E. (and technically A but that's clearly wrong :) ). . That leaves B and E. (and technically A but that's clearly wrong :) ).
Now E_2 > E_1 so the answer has to be less than 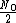 for positive epsilon. That leaves B. for positive epsilon. That leaves B.
Herminso
2009-09-22 19:08:11 |
I think the answer has to be more than 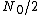 for for  > >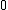 . Remember that the graph of . Remember that the graph of 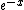 is below 1 for a is below 1 for a  positive. Thus positive. Thus 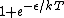 < <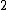 . The answer (B) holds. . The answer (B) holds.
|
shak
2010-10-10 09:25:14 |
what about D? it also goes to N/2 when epsilon=0.
why did u ignore it?
|
asdfuogh
2011-10-05 17:54:19 |
You're right, D) also goes to N0/2 when T=>inf. But then, we'd ignore that one when we think about T=>zero because that one blows up, and it shouldn't go bigger than N0.
|
|  | engageengage
2009-01-07 20:05:25 | I believe what you have down is not the correct fermi-dirac distribution, which shouldn't have a minus sign in front of the energy in the denominator. The other way to get this answer with few assumptions is just to say the partition function is:
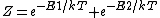
Then, to find the number of subsystems in E1, you have to multiply the probability of being in that state by the number of total particles. From basic boltzmann statistics, you know that:
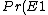 = \frac{e^{-E1/kT}}{Z} = \frac{e^{-E1/kT}}{e^{-E1/kT}+e^{-E2/kT}} )
Multiplying through by the inverse of the boltzman factor that was used, you get:
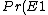 = \frac{1}{1+e^{-(E2-E1)/kT}} = \frac{1}{1+e^{-\epsilon/kT}} )
Multiply by the number of particles and you have answer (B)
antigravity
2010-11-09 08:22:29 |
I agree.. We cant assume Fermi Dirac distribution (It can be nything)..
However it has been mentioned tht the system is at high temperature where all the three distributions merge.
So take it as the Boltzmann one..
|
|  | Fv4
2008-10-04 09:43:14 | as epsilon -> 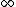 , number of subsystems at E1 should approach , number of subsystems at E1 should approach 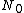 . Thus, only B) can be the answer. . Thus, only B) can be the answer. |  | hassanctech
2007-09-30 22:02:11 | Correct me if I'm wrong but if E2-E1 = e>0 then lets look at the limit as e --> infinity. This means that E2 is of infinite energy and you would expect all the sybsystems to be in the E1 state. Choice B is the only one for which e--> infinity reduces to N0.
Blue Quark
2007-10-31 19:22:45 |
Am I missing something?
As T approaches infinity all the particles should be in the highest energy state, E2.
For (b), as T approaches infinity the average number of particles in the lower energy state, E1, is equal to No. So as the temperature increases more particles are dropping to lower energy states?
|
Jeremy
2007-11-01 16:58:13 |
Blue Quark,
Check your math on the limit. The high temperature limit is in fact 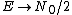 . Here's a qualitative idea of why it's true. At low temperatures, most of the subsystems are in the lowest energy state because there is not enough energy for a transition (taking . Here's a qualitative idea of why it's true. At low temperatures, most of the subsystems are in the lowest energy state because there is not enough energy for a transition (taking 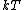 to represent the amount of energy available to the system). Of course, there may be a few subsystems in excited states, but I'm speaking about the typical case - what the "big picture" looks like. Well, as to represent the amount of energy available to the system). Of course, there may be a few subsystems in excited states, but I'm speaking about the typical case - what the "big picture" looks like. Well, as 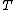 increases, the available energy increases, and more and more subsystems will be in their excited states. For increases, the available energy increases, and more and more subsystems will be in their excited states. For 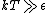 , the limitation imposed by energy is completely removed, so that it is equally likely to be in any of its available states. This is why we expect to find half of the subsystems in the lower state and half in the higher state. Also note that this macrostate maximizes entropy, whereas putting all subsystems in one state (for example the one with higher energy) will minimize entropy. And one last thing, this understanding allows you to answer #73 (from this test) immediately - no equations needed! , the limitation imposed by energy is completely removed, so that it is equally likely to be in any of its available states. This is why we expect to find half of the subsystems in the lower state and half in the higher state. Also note that this macrostate maximizes entropy, whereas putting all subsystems in one state (for example the one with higher energy) will minimize entropy. And one last thing, this understanding allows you to answer #73 (from this test) immediately - no equations needed!
|
Jeremy
2007-11-13 11:14:08 |
I finally found the other problem that my previous post churns out an instant answer for! It's GR8677 #67. So you can see everything one page, here's what it says:
__________
67. A large isolated system of 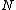 weakly interacting particles is in thermal equilibrium. Each particle has only 3 possible nondegenerate states of energies weakly interacting particles is in thermal equilibrium. Each particle has only 3 possible nondegenerate states of energies 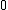 , ,  , and , and 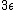 . When the system is at an absolute temperature . When the system is at an absolute temperature 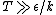 , where , where 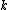 is Boltzmann's constant, the average energy of each particle is is Boltzmann's constant, the average energy of each particle is
(A) 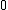
(B) 
(C) 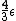
(D) 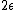
(E) 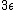
__________
Using the reasoning in my previous post, we know that the 3 states are equally occupied, so the average energy for any individual particle is just the average energy of the possible states: 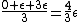 . .
Here " target="_blank">http://grephysics.net/ans/8677/67">Here is a link to the page discussing that problem, where others have already mentioned this shortcut.
|
Jeremy
2007-11-13 11:23:27 |
Why can I never get the link to work the first time? I must not be doing it right... but it works the second time. Anyone care to share a linking syntax that works?
Link
|
jmason86
2009-09-02 19:19:10 |
(D) would also satisfy the T-> inifnity then ave -> 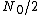 . I guess you just have to remember that there is always that minus sign in the exponential when talking about the partition fct or boltzmann distribution. . I guess you just have to remember that there is always that minus sign in the exponential when talking about the partition fct or boltzmann distribution.
|
|  | Richard
2007-09-13 23:48:09 | I too wanted to say that the posted solution is rather poor. This is a Boltzman stat. problem: The probability for a state is the Boltzman factor for that state divided by the Partition Function. What's with the, "let's assume that 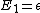 ?" ?"
evanb
2008-06-25 12:56:18 |
It turns out that it doesn't matter what 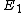 is equal to... it adds a factor of is equal to... it adds a factor of 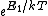 to the numerator and to all the factors in the denominator. Better off setting it to zero, in my opinion, but in terms of the physics it doesn't make one lick of difference: it's like setting your h in mgh potential energy to 0 on the ground. to the numerator and to all the factors in the denominator. Better off setting it to zero, in my opinion, but in terms of the physics it doesn't make one lick of difference: it's like setting your h in mgh potential energy to 0 on the ground.
See radicaltyro's comment on moonrazor's solution for evidence.
|
|  | georgi
2007-08-26 22:07:45 | the posted solution is actually just purely incorrect. a fermi dirac distribution assumes that the occupancy of a particular quantum state is either 0 or 1 in accordance with the pauli-exclusion principle. instead we are actually interested in a maxwell boltzmann distribution in which the particles (in our case subsystems) are distinguishable and any number can occupy either energy state. then we apply the partition function as posted by radicaltyro to obtain our solution.
FortranMan
2008-10-02 15:33:49 |
So because a system only has two states doesn't alone mean that it's Fermi-Dirac?
|
shak
2010-10-10 09:41:21 |
right!!
|
|  | moonrazor
2006-03-27 13:37:23 | (GR9277-71) Alternate Solution with less assumptions:
Using P(E) = (1/Z)exp[-E/kT] we have
P(E_1) = exp[-E_1/kT] / (exp[-E_1/kT] + exp[-E_2/kT])
= 1 / (1 + exp[-(E_1-E_2)/kT])
= 1 / (1 + exp[-\epsilon /kT])
LaTeX
\begin{eqnarray*}
P(E_{1}) &=& \frac{e^{-E_{1}/kT}}{e^{-E_{1}/kT} + e^{-E_{2}/kT}}\\
&=& \frac{1}{1 + e^{-(E_{2}-E_{1})/kT}}\\
&=& \frac{1}{1 + e^{-\epsilon/kT}}
\end{eqnarray*}
radicaltyro
2006-10-31 14:05:37 |
Hi moonrazor. Wrap your latex in single dollar signs.
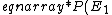 &=& \frac{e^{-E_{1}/kT}}{e^{-E_{1}/kT} + e^{-E_{2}/kT}}\\&=& \frac{1}{1 + e^{-(E_{2}-E_{1})/kT}}\\&=& \frac{1}{1 + e^{-\epsilon/kT}} \end{eqnarray*})
|
chemicalsoul
2009-11-04 20:58:32 |
This should be the standard solution Hon'ble Yosun.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
