|
GR9277 #65
|
|
|
|
|
Alternate Solutions |
QuantumCat
2014-09-16 15:16:59 | For anyone that wants to understand where the solution comes from without dimensional analysis, note first that the charge will not experience a force if it is at the origin, so we have to displace it a distance 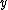 . Now, the electric field from each . Now, the electric field from each 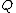 has a component in has a component in  and and 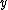 . The . The  components cancel, leaving only the components cancel, leaving only the 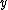 components, which act in the same direction, so you have an expression like this: components, which act in the same direction, so you have an expression like this:
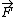 = = 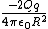 sin sin  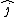 . .
Using geometry and our favorite small angle approximation for sine and tangent, we see that sin   tan tan   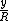 . .
This leads us to a very familiar relation:
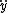 = = 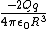 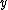
From which you can see that the two on top cancels and  jumps right out at you, leading to choice E. jumps right out at you, leading to choice E.
While it seems like a lengthy solution it's simple and straightforward, once you're comfortable with how it's done. |  | his dudeness
2010-10-09 08:06:47 | OK, so when you see the words "small oscillations", two formulas should pop immediately to mind:
(1) 
(2) 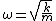
Looking at the answer choices, we see a bunch of forces everywhere. Substituting (1) into (2), we get  . The only answer with these units is (E) . The only answer with these units is (E)
(Since we are doing dimensional analysis and only care about getting the correct units, it is quite OK to play fast and loose with the equations like this :-) ).
|  | daschaich
2005-11-11 16:55:28 | Oh dear. Looks like I missed a dollar sign or backslash or something. Let's try this again...
(A) and (B) have dimensions of 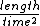 , (C) has dimensions of , (C) has dimensions of 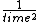 , (D) has dimensions of , (D) has dimensions of 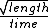 and only (E) has dimensions of and only (E) has dimensions of  appropriate for a frequency. appropriate for a frequency. |  |
|
|
Comments |
memyselmineni
2014-11-27 05:12:26 | This is application of coluomb law. For different charge positions and other EM questions pls refer to a wonderful bookhttp://www.amazon.com/Physics-Mathematica-Jude-Ndubuisi-Onicha/dp/1499691920/ref=sr_1_fkmr1_1?s=books&ie=UTF8&qid=1401627044&sr=1-1-fkmr1&keywords=physics+mathematica++2nd+edition+by+onicha+jude |  | QuantumCat
2014-09-16 15:16:59 | For anyone that wants to understand where the solution comes from without dimensional analysis, note first that the charge will not experience a force if it is at the origin, so we have to displace it a distance 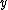 . Now, the electric field from each . Now, the electric field from each 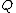 has a component in has a component in  and and 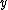 . The . The  components cancel, leaving only the components cancel, leaving only the 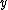 components, which act in the same direction, so you have an expression like this: components, which act in the same direction, so you have an expression like this:
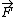 = = 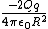 sin sin   . .
Using geometry and our favorite small angle approximation for sine and tangent, we see that sin   tan tan    . .
This leads us to a very familiar relation:
 = = 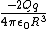 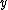
From which you can see that the two on top cancels and  jumps right out at you, leading to choice E. jumps right out at you, leading to choice E.
While it seems like a lengthy solution it's simple and straightforward, once you're comfortable with how it's done. |  | his dudeness
2010-10-09 08:06:47 | OK, so when you see the words "small oscillations", two formulas should pop immediately to mind:
(1) 
(2) 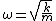
Looking at the answer choices, we see a bunch of forces everywhere. Substituting (1) into (2), we get  . The only answer with these units is (E) . The only answer with these units is (E)
(Since we are doing dimensional analysis and only care about getting the correct units, it is quite OK to play fast and loose with the equations like this :-) ).
flyboy621
2010-10-22 13:44:31 |
+1
|
|  | violet
2008-10-19 20:04:50 | |  | FortranMan
2008-10-01 20:02:42 | recall the period for an oscillating pendulum, sort out the analogies for acceleration and length, invert, and BOOM, problem solved. |  | madfish
2007-11-01 11:09:08 | Thanks, daschaich your solution seems the fastest, I doubt I would think to look at the differential motion equation as I would assume the y-components of this system would cancel by symmetry. |  | 94709
2007-10-22 23:42:37 | Not sure what "compensating" means for me. A bit detailed solution;
When a charge 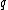 is along is along 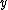 -axis, and when it is at very close to the origin (which is the case for small oscillation), let -axis, and when it is at very close to the origin (which is the case for small oscillation), let  be an angle between two lines; x-axis and a line connecting be an angle between two lines; x-axis and a line connecting 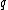 and and 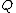 . .
Then, by small angle approximation,
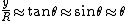
The distance between 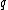 and and 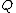 is, therefore, is, therefore,
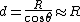
Magnitude of force on charge 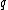 by ONE by ONE 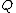 along y-axis is, therefore, along y-axis is, therefore,

Using Newton's 2nd Law (or SHO differential equation),
}{m})
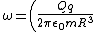^{\frac{1}{2}})
Hence, choice (E). All this can be done in a minute for sure, but dimentional analysis is strongly recommended as daschaich mentions.
sina2
2013-10-06 07:09:05 |
I did like you.
|
|  | nitin
2006-11-20 03:39:20 | Magnitude of force acting on charge -q:
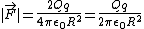 . .
Now,
 , ,
so that
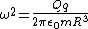 . .
The answer (E) follows.
georgi
2007-08-26 21:02:10 |
i don't think this solutions works even though it gives the right answer since you are using the formula for circular motion and centripetal acceleration.
|
neutrinosrule
2008-10-04 18:40:03 |
I'm only saying this because you did get the right answer, but it sort of makes sense (even though it's not circular motion) because oscillations are similar to circular motion... the shadow of an object in vertical circular motion is often used to introduce oscillations. The time it takes for an object to get from one side of a circle to the other in circular motion would be the same as the time for an oscillation, so since we're dealing with frequency, maybe this is a correct way to simplify and approximate this problem...
|
conrad
2009-11-03 19:58:29 |
Remember that 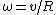 and and 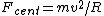 . Therefore . Therefore 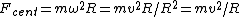 . Memorizing this relation saves lots of time. This is a great approach to the problem. . Memorizing this relation saves lots of time. This is a great approach to the problem.
|
|  | daschaich
2005-11-11 16:55:28 | Oh dear. Looks like I missed a dollar sign or backslash or something. Let's try this again...
(A) and (B) have dimensions of 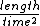 , (C) has dimensions of , (C) has dimensions of 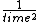 , (D) has dimensions of , (D) has dimensions of 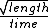 and only (E) has dimensions of and only (E) has dimensions of  appropriate for a frequency. appropriate for a frequency.
daschaich
2005-11-11 16:52:45 |
Can also be done using dimensional analysis. Since 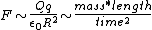 , (A) and (B) have dimensions of , (A) and (B) have dimensions of 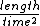 , (C) has dimensions of , (C) has dimensions of 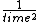 , (D) has dimensions of , (D) has dimensions of  sqrt{length}}{time} sqrt{length}}{time} has dimensions of ) \frac{1}{time}$ appropriate for a frequency. \frac{1}{time}$ appropriate for a frequency.
|
jmason86
2009-09-06 16:19:13 |
word up. This is the best way to solve this problem under time pressure.
|
koppes
2009-10-31 14:07:08 |
What is the result of dimensional analysis for Coulombs or Amps?
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
