|
GR9277 #64
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
NoPhysicist3
2017-03-23 12:31:21 | The words \"certain region\" are VERY confusing. However, when choosing between B and E, one should keep in mind that it is unlikely for ETS to consider a correct answer containing ultimate statements. Therefore B is the only correct. |  | Naismith
2011-10-10 04:30:08 | What do they mean by "in a certain region" ? In my opinion, it is always possible to find a region small enough so that it doesn't contain any charges, therefore charge density. The charge then will be outside the region...
h.fei10
2012-11-04 07:42:12 |
That's not possible. The electric field pevades this certain region, so does the charge.
|
calcuttj
2014-09-03 17:57:04 |
Think about the field inside a cylinder of constant charge density.
The cylinder has radius R, constrain r < R such that
|E|* r^2d = r^2d =   r^3d r^3d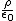
(d is the length of our Gaussian cylinder)
|E| =  r r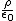
The region could be the z axis inside the cylinder
Not necessarily the only charge distribution to create E =kz, and this definitely doesn't prove there is ALWAYS a distribution to create a field like this, but it definitely disproves that the field is impossible
Now think about this. If there wasn't a charge density in the region. shouldn't the field be decreasing (i.e. E=k/z)?
|
calcuttj
2014-09-10 16:36:07 |
I made a mistake in my last comment, ignore it.
|
|  | r10101
2007-10-27 16:32:37 | Why does a small region of vacuum near the surface of an infinite charged plate (with constant  = E = E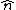 normal to the surface) not satisfy this question, making answer (E) correct? normal to the surface) not satisfy this question, making answer (E) correct?
panos85
2007-10-31 05:12:32 |
It says 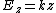 , not , not  . The electric field near the surface of a conductor is constant, while the field in this problem is not. . The electric field near the surface of a conductor is constant, while the field in this problem is not.
|
tonyhong
2008-10-25 01:54:24 |
this is a trap...
|
|  | sharpstones
2006-12-01 10:25:11 | how could you possibly construct a charge density that would make such an E field?
mhas035
2007-04-04 23:58:56 |
Remember that it says that the field is only in a certain region. We just need the region to be small with a relatively large charged plane of constant charge density.
|
evanb
2008-06-24 11:56:52 |
How about a uniform-density infinite-plane slab. So, it would be thick and the region of interest would be from the middle of the slab to the edge of the slab.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
