|
GR9277 #5
|
|
|
Problem
|
|
\prob{5}
The magnitude of the Earth's gravitational force on a point mass is F(r), where r is the distance from the Earth's center to the point mass. Assume the Earth is a homogenous sphere of radius R.
Suppose there is a very small shaft in the Earth such that the point mass can be placed at a radius of R/2.
What is }{F(R/2)}$)
- 8
- 4
- 2
- 1/2
- 1/4
|
Mechanics }Gauss Law }Gauss Law
The inverse-square law doesn't hold inside the Earth, just like how Coulomb's law doesn't hold inside a solid sphere of uniform charge density. In electrostatics, one can use Gauss Law to determine the electric field inside a uniformly charged sphere. The gravitational version of Gauss Law works similarly in this mechanics question since 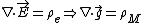 , where , where 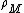 is the mass density of is the mass density of 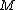 . In short, the gravitational field . In short, the gravitational field 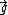 plays the analogous role here as that of plays the analogous role here as that of  Thus, Thus, 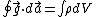 . .
So, for 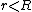 , , =\rho \frac{4}{3}\pi r^3 \Rightarrow g= r\frac{\rho}{3}) , where one assumes , where one assumes 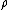 is constant. is constant.
To express the usual inverse-square law in terms of 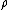 , one can apply the gravitational Gauss Law again for , one can apply the gravitational Gauss Law again for 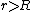 , , =\rho \frac{4}{3}\pi R^3 \Rightarrow g=\frac{R^3}{r^2}\frac{\rho}{3})
Since 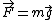 Therefore, Therefore,
}{F(R/2)}=2.
)
which is choice (C).
|
|
|
Alternate Solutions |
gravity
2010-11-07 17:32:13 | You know from the last problem that the answer would be 4 if the the earth had a radius of R/2. But since you're going into the earth, the mass above you pulls you up, so the force gets smaller as you go in. Therefore the ration gets smaller than 4 - and it's obviously not less than one, so the answer is 2.
I'm learning this trick on these tests: Always look at the answers given before going through the logic of figuring out the solution. Sometimes it's just obvious. |  | Anastomosis
2008-04-09 08:15:40 | I did something similar, but I wasn't thinking of Gauss' law.
I just figured that since the mass density 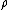 was homogenous throughout, then the mass of the Earth at any point was homogenous throughout, then the mass of the Earth at any point  = \rho V = \rho \frac{4}{3} \pi R^3) . .
So:  = \frac{G \rho \left( \frac{4}{3} \pi R^3 \right) }{R^2})
And:  = \frac {G \rho \left( \frac{4}{3} \pi (\frac{R}{2})^3 \right) }{(\frac{R}{2})^2})
Cancel out common terms and you have:
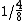
which is 2.
|  |
|
|
Comments |
bonghan_lee27
2016-05-22 17:31:13 | Tricky question. I had missed out about the gravitational Gauss Law perspective! |  | cczako
2013-10-15 17:50:49 | A quick and easy way to do this is to remember that the gravitational force (and coulomb force for that matter) has a dependence on r inside a sphere and 1/(r^2) outside the sphere. Thus to solve this:
F(R)/F(R/2)= R/(R/2)=2
|  | kstephe6
2012-11-04 16:55:22 | ONLY FAST ANSWERS MATTER.
At (1/2) the radius, you only get (1/8) of the Earth's mass but gravity is 4 times a stronger. Just combine the two results...
(1/8)*(4) = 2
...to get the answer. |  | gravity
2010-11-07 17:32:13 | You know from the last problem that the answer would be 4 if the the earth had a radius of R/2. But since you're going into the earth, the mass above you pulls you up, so the force gets smaller as you go in. Therefore the ration gets smaller than 4 - and it's obviously not less than one, so the answer is 2.
I'm learning this trick on these tests: Always look at the answers given before going through the logic of figuring out the solution. Sometimes it's just obvious.
carle257
2010-11-10 16:02:59 |
This isn't quite right. The earth above does pull you up, but the other side pulls stronger since you are closer. The explanation falls out of the shell theorem (or equivalently Guass's law for gravity which says that only the mass internal to the surface contributes to the force. Thus you would need to do the integral, or just remember that the force inside a homogeneous sphere has a linear dependence on radius.
|
Quark
2011-10-25 12:39:54 |
Actually I don't believe that the point mass would feel a gravitation pull from the any part of the earth outside of the R/2 radius. It would only feel the gravitation pull from the mass of the earth inside R/2. Very similar to the electrostatic case. I would say this is correlated with equipotentials.
|
|  | CarlBrannen
2010-10-07 17:48:13 | Like ETS thinks that the density of the earth doesn't depend on distance. The actual answer might be closer to 4 than 2 since the steel core has a density around 3x that of the mantle. |  | tsharky87
2009-10-29 13:00:04 | I suppose this applies to uniformly charged sphere's as well:
I'm confused as to why we in Anastomosis' solution you can just entirely ignore all of the mass that is ABOVE R/2. Intuitively, it seems like the mass above R/2 has it's own gravitational pull which will effectively make you lighter than if you were just standing on a planet of Earth's density that has a radius R/2.
kroner
2009-10-29 13:53:00 |
The net effect of all the mass above R/2 is zero. This is a result of what's called the shell theorem. It's pretty easy to show with Gauss' Law. Imagine a spherical Gaussian surface S at radius R/2. The net gravitational flux through S only depends on the amount of mass M inside the surface (flux is 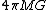 ). By symmetry, the gravitational field at every point on S is equal so ). By symmetry, the gravitational field at every point on S is equal so  where A is the area of S, where A is the area of S, ^2) . .
|
|  | engageengage
2009-01-08 17:01:04 | quick way to do this is to remember that inside the earth (or an insulating sphere of charge) the gravitational (or electric) field will be linear, starting from 0 at R = 0 (since an infinitely small sphere encloses no mass/charge). Therefore the force at R it will be double what it was at R/2, since it has increased linearly.
hoboboxer
2013-04-15 18:08:21 |
I like it. Remember this and "get two birds stoned at once"
|
|  | Anastomosis
2008-04-09 08:15:40 | I did something similar, but I wasn't thinking of Gauss' law.
I just figured that since the mass density 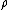 was homogenous throughout, then the mass of the Earth at any point was homogenous throughout, then the mass of the Earth at any point  = \rho V = \rho \frac{4}{3} \pi R^3) . .
So:  = \frac{G \rho \left( \frac{4}{3} \pi R^3 \right) }{R^2})
And:  = \frac {G \rho \left( \frac{4}{3} \pi (\frac{R}{2})^3 \right) }{(\frac{R}{2})^2})
Cancel out common terms and you have:
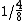
which is 2.
caffeinated
2008-04-09 08:51:51 |
I like your solution. I just wish I could understand the question.
|
lattes
2008-08-23 11:46:01 |
caffeinated. The question basically ask you the ratio of ) and and ) (recall that the problem states that (recall that the problem states that 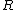 is the Earth's radius, so is the Earth's radius, so 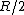 is inside Earth) . Anastomosis' solution consists on writing is inside Earth) . Anastomosis' solution consists on writing ) as as =\frac{Gm}{r^2}=\frac{G\rho V}{r^2}) and solving for and solving for 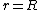 and and 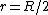 . .
|
lattes
2008-08-23 11:49:12 |
typo: =\frac{GmM}{r^2}=\frac{Gm\rho V}{r^2})
|
ramparts
2009-08-09 16:06:55 |
I did it the same way, but with a little less algebra. Just note that your F(R) equation simplifies to:
 = k R)
Where k is some collection of constants. That way you're not wasting time at the test writing down G's, rhos, and all the rest ;)
|
grace
2010-11-12 12:43:35 |
I think this is easy way.
|
|  | jcain6
2005-11-14 18:15:53 | 2R is not a choice. 2 is choice (c). Using the method outlined above I am still getting 1/4.
for F(R) = const/3R^2
F (R/2) = const/3(R/2)^2
F(R) / F(R/2) = 1/4
What am I doing wrong
yosun
2005-11-14 20:44:46 |
jcain6: thanks for the typo-alert; it has been corrected.
note that in the method above, one evaluates /F(R/2)) where where =R^3\rho/(3r^2)\Rightarrow F(R)=\rho R/(3)) and and =\rho r/3 \Rightarrow F(R/2)=\rho (R/2)/3) . .
jcain6: you seem to be using the wrong formulae. note carefully how the R's must cancel in the individual force equations before you plug in the ratio.
|
yosun
2005-11-14 20:53:20 |
note that in my ) equations below, I've neglected the mass m, so technically equations below, I've neglected the mass m, so technically  \rightarrow g(r)) . (The masses cancel in the ratio at the end, so this does not make a difference in the final answer.) . (The masses cancel in the ratio at the end, so this does not make a difference in the final answer.)
|
jcain6
2005-11-17 10:15:23 |
I see what I did. Thanks yosun.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
