|
GR9277 #6
|
|
|
Problem
|
|
\prob{6}
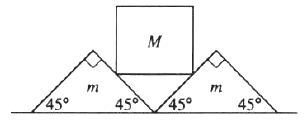
Two wedges, each of mass m, are placed next to each other on a flat floor. A cube of mass M is balanced on the wedges as shown above. Assume no friction between the cube and the wedges, but a coefficient of static friction  between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges? between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges?
-

-
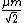
-
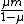
-
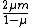
- All M will balance.
|
Mechanics }Method of Sections }Method of Sections
By symmetry, one can analyze this problem by considering only one triangular wedge. The normal force on one wedge is just 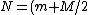g) , since by symmetry, the wedge (m) carries half the weight of the cube (M). The frictional force is given by , since by symmetry, the wedge (m) carries half the weight of the cube (M). The frictional force is given by 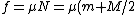g) . .
Sum of the forces in the horizontal-direction yields 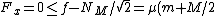g - Mg/2) for static equilibrium to remain valid. (Note that the normal force of the cube is given by for static equilibrium to remain valid. (Note that the normal force of the cube is given by 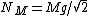 since, summing up the forces perpendicular to the plane for M, one has, since, summing up the forces perpendicular to the plane for M, one has, =Mg/2) . Also, note that it acts at a 45 degree angle to the wedge.) . Also, note that it acts at a 45 degree angle to the wedge.)
Solving, one has g \geq Mg/2 \Rightarrow M \leq \frac{2\mu m}{1-\mu}) . .
(In a typical mechanical engineering course, this elegant method by symmetry is called the method of sections.)
|
|
|
Alternate Solutions |
packinski
2011-08-01 16:48:44 | We can eliminate several answer choices here using common sense.
Note that in the limit of 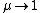 , , 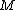 is expected to go to is expected to go to  as well. That's is , it would require a very, very large mass to move the wedges apart, in this surface with very very high coefficient friction constant. as well. That's is , it would require a very, very large mass to move the wedges apart, in this surface with very very high coefficient friction constant.
Only answer choices (C) and (D) satisfies this condition. Since the system is symmetric one could guess answer choice (D) which has a factor of  . . |  |
|
|
Comments |
droosenoose
2019-10-18 00:46:50 | Consider conservation of energy. \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\r\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\n\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\r\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\nIf the block slides at a constant rate down the wedges a distance d then the potential energy lost is Mgd which goes to the friction (2m+M)ug*x but since 45 degree wedges x=d and you get M = 2um/(1-u) |  | kstephe6
2012-11-04 17:04:47 | ONLY FAST ANSWERS MATTER!
Due to statics, the total normal force MUST be (2m+M)g
(FORGET RESOLVING VECTORS)
So the friction force for static equilibrium MUST be (mu)*(2m+M)g...
...and this force must hold the block up against gravity, and we have (mu)*(2m+M)g = Mg
Solve for M and go!
Nezumi
2013-06-24 12:47:26 |
Excellent solution!!!
|
|  | greatspirits
2012-10-29 15:05:38 | Symmetry is useful for sure. Then consider the verticle force on the wedge is  . Then the static friction force on the ground is . Then the static friction force on the ground is 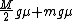 This must exceed the horizontal force which is also magnitude This must exceed the horizontal force which is also magnitude  Then solve Then solve 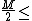 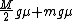 for for 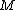 . . |  | Earthysmell
2012-09-28 10:40:18 | Again to clarify, M exerts the full force (Mg) on Both wedges (after which components can be resolved).
so correct answer is D
greatspirits
2012-10-29 14:43:32 |
Careful there,... ever try to lift a circular hot tub. Imagine lifting it with three people in an equilateral triangle. Then imagine lifting it with 6 people in an equilateral hexagon. The latter arrangement is easier...force divides between contact points.
|
|  | erore
2011-11-04 14:08:36 | For me the solution shown is pretty confusing. For some reason it works but it definitely eludes me. In the case of the normal force leading to frictional force, the author uses only M/2 while to calculate the force that moves the wedge, the whole M is used. I do not know the method of sections but both forces (the frictional and the one that tries to move the wedge) are due to a single force - the cube's acting on the wedge due to gravity.
Rosenlicht
2011-11-08 11:59:13 |
The horizontal component here is Mg*tan( /4) so you just get Mg on the left hand side. Since we are using symmetry, you're left with Mg = u(M+2m)g. Solve for M. /4) so you just get Mg on the left hand side. Since we are using symmetry, you're left with Mg = u(M+2m)g. Solve for M.
|
walczyk
2012-10-15 10:48:42 |
Method of Sections does not work in this example because the full mass M exerts the same horizontal force on each wedge, using M/2 on just one wedge yields an incorrect result.
The block M exerts a force ) on each wedge perpendicular to the plane of each wedge. We break these up into x and y components, so for the first wedge we will have on each wedge perpendicular to the plane of each wedge. We break these up into x and y components, so for the first wedge we will have 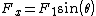 = Mgcos(\theta)sin(\theta)) and similarly and similarly 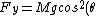) . .
Doing the math and simple trig substitutions we get our answer to the general system of two wedges of equal mass and incline:
 - \mu sin(2\theta)}) which simplifies to our answer when we use which simplifies to our answer when we use 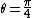
|
|  | packinski
2011-08-01 16:48:44 | We can eliminate several answer choices here using common sense.
Note that in the limit of 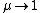 , , 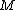 is expected to go to is expected to go to  as well. That's is , it would require a very, very large mass to move the wedges apart, in this surface with very very high coefficient friction constant. as well. That's is , it would require a very, very large mass to move the wedges apart, in this surface with very very high coefficient friction constant.
Only answer choices (C) and (D) satisfies this condition. Since the system is symmetric one could guess answer choice (D) which has a factor of  . .
NoPhysicist3
2017-03-23 08:42:15 |
Taking limits in this task is a perfect way to solve the problem (and I think it is what GRE wants to test here), however it could be complicated to guess the factor of 2 between C and D.\r\nMore explicit reasoning is the following: since we have two triangle wedges, the big mass M would be distributed between both, therefore the maximum mass M would be twice of that in answer C, therefore leaving us with the correct D.\r\n
|
|  | Da Broglie
2011-04-06 15:37:10 | Just another way to solve this problem.
Follow Yosun's advice and only look at one of the wedges.
By symmetry half the block is supported by each wedge. Since the block makes a 45 degree angle with the wedge, half of that mass is supported by the normal force and the other half by the friction force.
the equations go:
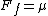 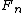 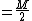 
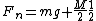
plugging equation 2 into 1 we get:
=\frac{M}{2}\frac{1}{2})
rearranging and solving for M we get:
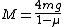 however the block is supported by two wedges we divide by two to get however the block is supported by two wedges we divide by two to get 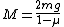 which is choice (D) which is choice (D)
rizkibizniz
2011-11-05 02:05:10 |
I think this solution is the correct reasoning for the answer. Yosun's reasoning is somewhat incorrect i think, she uses the wrong value of 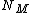 . In the one wedge system, shouldn't . In the one wedge system, shouldn't 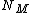 be be 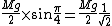 as has been used by Da Broglie?rnrn as has been used by Da Broglie?rnrn
|
rizkibizniz
2011-11-05 02:08:58 |
Actually, never mind. I don't know what I'm talking about. but I am still confused of Yosun's answer and I still am more fond of Da Broglie's answer than hers.
|
|  | walczyk
2011-03-18 20:09:37 | I am not sure if I agree with the logic of the approved solution, in regards to the method of sections, but it does work out. The problem is not difficult to solve directly however. The block rests at a 45 degree angle on both blocks, and therefore exerts a force Mgsin(pi/4) or Mgcos(pi/4) (depending on where you take the angle form), so Mg/sqrt(2), where the force is applied perpendicular to the ramps of the wedges. Now you then break up this force into horizontal and vertical components by applying sin(pi/4) and cos(pi/4) again to the applied force. That is how the sqrt(2) term becomes 2, because the original weight of the block acts at a 45 degree angle to the wedges, and then that force is split up into components, which are luckily 45 degrees to this force once again. Plug and chug and get the answerrr. This wasn't a very graceful explanation, but it correctly explains the forces of the system |  | Albert
2009-10-20 01:30:08 | In case someone is confused about resolving the forces into components, you don't really have to, a simpler version is this:
The total force trying the move the wedges sideways is Mg.
The total amount of force acting downward is (M+2m)g.
And therefore, the total opposing frictional force is mue*(M+2m)g.
Simply equate the two and you get the answer.
nyuko
2009-10-30 09:34:59 |
I suppose you got it by luck.
Simply change the wedges with angles  then the answer would become: then the answer would become:
\leq 2 \mu m)
|
nyuko
2009-10-30 20:26:41 |
Sorry, should be \leq 2\mu m)
|
Albert
2009-11-02 13:57:37 |
You see, that is indeed the beauty of my idea. I never had to resolve anything into components. And hence, no matter the angle, or whatever you replace it with, the answer shan't change :)
|
nyuko
2009-11-04 07:07:11 |
Maybe you misunderstood me? I showed above that  comes in when the angles of the wedges are not comes in when the angles of the wedges are not 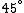 but but  . I meant to say that the maximum of . I meant to say that the maximum of 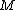 does depend on the angle... does depend on the angle...
|
nyuko
2009-11-05 23:53:28 |
Look at it this way:
you're right that the total downward force is (M+m)g.
BUT the force trying to move the wedge sideways depends on the angle. Only when the angle is 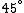 then the vertical component equals horizontal component. then the vertical component equals horizontal component.
|
fredsp7
2010-03-08 09:09:31 |
I tryied to calculate like you said with any angle \theta but my answer came as being: M\leq \frac{2\mu m}{(2\cos \theta \sen \theta - \mu)} and it also provides the correct answer with \theta=45
|
fredsp7
2010-03-08 09:27:42 |
I tryied to calculate like you said with any angle \theta but my answer came as being: M\leq \frac{2\mu m}{(2\cos \theta \sen \theta - \mu)} and it also provides the correct answer with \theta=45
|
fredsp7
2010-03-08 14:18:38 |
Sorry about the messages, first time. Real Message:
I tryied to calculate like you said with any angle  but my answer came as being: but my answer came as being: }) and it also provides the correct answer with and it also provides the correct answer with 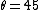
|
|  | caffeinated
2008-04-04 08:49:12 | So M is exerting both vertical and horizontal components of Mg/2.???
Poop Loops
2008-10-05 12:57:13 |
Look at it this way:
Each wedge feels a force M/2 downwards, since each is holding up half of the block M.
But, the wedges cannot exert forces straight up, they can only exert them in directions normal to their planes. So, if we take the left wedge, it can only push on Block M up+right, i.e. perpendicular to the plane that Block M is touching.
And since this is a 45 degree angle, it has to push on Block M with equal force up AND right. One can't be greater than the other, purely because of the angle involved. So we know it is pushing up at M/2, therefore it has to push Right at M/2 also. The right wedge is the same, except that it is pushing up + left, so that the right and left wedges both push on Block M with M/2 force, but in opposite directions left and right, so that Block M stays still and only slides down.
Now, since the wedges are pushing on Block M with M/2, it is pushing back on them with the same force.
|
his dudeness
2010-09-03 18:37:11 |
great username, great explanation
|
|  | caffeinated
2008-04-04 08:42:07 | I don't understand why the "normal" force of M (which is at a 45 degree angle) on one of the wedges is greater than Mg/2. (Mg/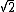 is greater than Mg/2.) This does not make sense to me. is greater than Mg/2.) This does not make sense to me.
ehab
2008-04-07 07:03:02 |
Imagine the large block M to have its mass concentrated in the middle at its centre of gravity. Now analyze its wiegth (Mg) into two components, each of which is normal to the side of one wedge. So each component is Mg cos theta.
Now, this component can be analyzed normally and horizontally, the normal component is:
Mg cos theta (cos theta)= Mg (cos theta)^2
That's it!
|
|  | bucky0
2007-10-03 19:35:18 | To clarify, the correct answer is (D) |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
