|
GR9277 #43
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
matweiss
2010-11-13 18:02:20 | This question can pretty easily be answered by eliminating all of the wrong answers.
A) Why would momentum be ignorable? (this is a bogus postulate) WRONG
B) Possibly
C) How could somethings momentum be undefined? This makes no sense at all WRONG
D) This is the system's equation of motion. There is, by definition, more to the EQN of motion than just the momentum WRONG
E) The hamiltonian has units of energy. Momentum does not. WRONG
We are left with B, which also seems reasonable |  | istezamer
2009-11-06 11:21:50 | If someone recalls Noether theorem!! If a system has a continuous symmetry property, then there are corresponding quantities whose values are conserved in time... So the generalized momentums are conserved... |  | $null
2009-10-28 16:03:39 | Problem definition should appear as 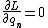 . Currently it appears as . Currently it appears as 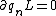 . .
neon37
2010-11-11 22:26:29 |
Its the same thing in tensor notation. It should be actually, 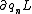 and not and not 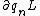 . In order to illustrate difference, . In order to illustrate difference, 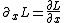 not not 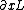 . .
|
|  | FortranMan
2008-09-27 15:04:58 | option (A) pisses me off. "An ignorable coordinate"? I have enough problems trying to approximate in physics as it is, but I suppose one was supposed to pick up on the definition that both are referred to as "generalized" and hence equal in importance to not neglect. But still, in an exam where I must do numerical approximations because I can't use a calculator, the last thing I need is more vague shit.
CaspianXI
2009-03-19 16:29:47 |
A vague answer is rarely the correct one. If it's too vague for you to figure out whether it's correct, rule it out.
|
gt2009
2009-05-20 08:12:20 |
Both those terms have a definition and are not vague. Look it up an a classical mechanics text.
|
gt2009
2009-05-21 20:34:45 |
Sorry, here is a more helpful post.
Generalized corrdinates - Any set of coordinates that completely specifies the state of a system. For a system with N degrees of freedom and S constraints, you need N - S independent coordinates to completely specify the state of the system. These can be anything you like, as long as there are N - S of them and they are independent. For example, for a plane pendulum you have 2 DOF - 1 constraint (constant length), so you only need one generalized coordinate, a good choice being the angle it makes from its equilibrium position, or you could still choose either x or y since they are not independent due to the constraint, or anything else you like.
An ignorable coordinate (also called a cyclic coordinate) is a coordinate that does not appear in the Lagrangian (or therefore H). However the generalized velocity related to this coordinate is in general still present. Ex - free particle, x is cyclic but 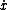 is still present. The conguate momentum of the ignorable coordinate, ie is still present. The conguate momentum of the ignorable coordinate, ie  L/ L/ 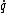 will be a constant of motion, as is the case for a free particle (or this problem). will be a constant of motion, as is the case for a free particle (or this problem).
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
