\prob{2}
The longest wavelength x-ray that can undergo Bragg diffraction in a crystal for a given family of planes of spacing d is
- d/4
- d/2
- d
- 2d
- 4d
|
Atomic }Bragg Diffraction }Bragg Diffraction
Recall the Bragg Diffraction dispersion relation,
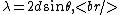
thus the maximal wavelength  would be would be 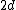 , choice (D). (One can derive that even if one does not remember the formula. Consider two lattice planes. View them from the side so that they appear as two parallel lines. A wave would hit the both planes at, say, an angle , choice (D). (One can derive that even if one does not remember the formula. Consider two lattice planes. View them from the side so that they appear as two parallel lines. A wave would hit the both planes at, say, an angle  from the normal. The wave that reflects off the bottom lattice will have to travel an extra distance, relative to the wave hitting the top plane, equal to from the normal. The wave that reflects off the bottom lattice will have to travel an extra distance, relative to the wave hitting the top plane, equal to 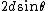 .) .)
|
