nirav_605
2012-03-19 17:31:20 | Isn't is suppose to be..
E_n = E_1 * (Z)^2/n^2
Not
E_n = Z^2/(n^2 * E_1) |  |
Poop Loops
2008-10-05 12:40:06 | Basically, you are using Moseley's Law:
http://en.wikipedia.org/wiki/Bohr_model#Moseley.27s_law_and_calculation_of_K-alpha_X-ray_emission_lines
Where a K X-ray is emitted when you go from 2nd shell down to 1st shell.
So you take ^2*(1-\frac{1}{4})) with some constant out front that will cancel to get the energy for an atom, and Z = 6 for one and Z = 12 for the other, so you get with some constant out front that will cancel to get the energy for an atom, and Z = 6 for one and Z = 12 for the other, so you get
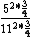
And of course 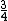 cancels, so you get cancels, so you get 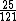 which is almost 1/5, not quite the right answer, but close enough to 1/4. which is almost 1/5, not quite the right answer, but close enough to 1/4. |  |
Jeremy
2007-10-30 12:18:12 | Typo: 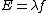 should be should be 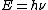 (...though I don't see why this is needed in solving the problem). (...though I don't see why this is needed in solving the problem).
A nice, concise background is given on Wikipedia about Moseley's " target="_blank">http://en.wikipedia.org/wiki/Moseley%27s_law">Moseley's Law. In particular, the derivation section ties this back into the more familiar realm of Bohr theory.
Jeremy
2007-10-30 12:28:40 |
Link
|
|  |
Mexicana
2007-10-04 13:38:09 | The way to justify the method of Yosun is to realise that K shell X-rays are produced by the transition of atomic electrons which were on the highest energy levels of that atom. These jump to the lowest level (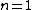 ) and since ) and since 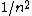 is small for large , one can readily neglect its contribution to the total transition energy and only account for the final level they jumped to, i.e. for is small for large , one can readily neglect its contribution to the total transition energy and only account for the final level they jumped to, i.e. for |  |
Mexicana
2007-10-04 13:36:36 | The way to justify the method of Yosun is to realise that K shell X-rays are produced by the transition of atomic electrons which were on the highest energy levels of that atom. These jump to the lowest level () and since is small for large , one can readily neglect its contribution to the total transition energy and only account for the final level they jumped to, i.e. for 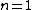 |  |
Mexicana
2007-10-04 13:35:02 | The way to justify the method of Yosun is to realise that K shell X-rays are produced by the transition of a atomic electron which were on the highest levels of that atom. These jump to the lowest level (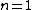 ) and since ) and since 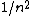 is small for large is small for large  , one can readily neglect its contribution to the total transition energy. , one can readily neglect its contribution to the total transition energy. |  |
kolahalb
2007-09-25 11:08:54 | Bohr's law fits here well.But C or, Mg are not Hydrogen like systems.Preferably we can use Moseley's law.
$\sqrt{ν}$=a(Z-b) where for K lines,b~1.
And,E=hν of course
This calculation shows that E(C)/E(Mg)=25/121
~(1/5)
Which rather matches (A)
sidharthsp
2008-10-01 21:36:27 |
that seems very just....
|
|  |
