|
GR8677 #77
|
|
|
|
|
Alternate Solutions |
ethanque
2015-08-12 08:54:41 | Hooke's Law and Work Energy Theorem:
I couldn't remember my wave equations right away so I used the work energy theorem imagining this is a SHO/spring:
The particle has zero kinetic energy when 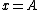 , and it is subject to the force , and it is subject to the force 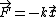 as it travels from as it travels from 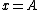 to to 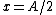 . i.e. the spring does work on the particle. . i.e. the spring does work on the particle.
So, integrate
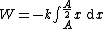
![\frac{1}{2} mv^2 = -k \frac{1}{2}[\frac{A^2}{4} - A^2]](/cgi-bin/mimetex.cgi?\frac{1}{2} mv^2 = -k \frac{1}{2}[\frac{A^2}{4} - A^2] )
Recall that 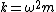 . Then . Then
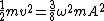
Recall that 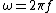 . Then . Then
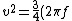^2 A^2 )
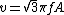 , which is option (B). , which is option (B).
Badda-bing badda-boom! |  | wittensdog
2009-10-07 18:32:43 | Yet another solution...
You can easily find that the argument of the sine function must be 1/2. If you know the value of a sine function at one point, you immediately know the value of cosine, since,
cos^2 + sin^2 = 1 ==>
cos = sqrt ( 1 - sin^2 ) ==>
cos = sqrt(3) / 2
which then you just plug right into the velocity formula. It's similar to the original solution, but you don't need to remember what angles correspond to what values of sine and cosine. |  | lattes
2008-08-07 13:08:18 | Another to solve is: consider Let =A\cos{\omega t}) and and =-A\omega\sin{\omega t}) . Squaring both equation and summing them we get: . Squaring both equation and summing them we get: }^{2}+{(\frac{v}{A\omega})}^{2}=1) . Now let . Now let 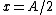 and solve for and solve for  . Thus . Thus 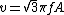 . (you should remember that . (you should remember that  !). A little bit longer solution, but it works. !). A little bit longer solution, but it works. |  | rreyes
2005-10-31 08:06:24 | an alternative solution is conservation of energy
1/2kA^2=1/2kx^2+1/2mv^2
plugging in x=A/2 gives
v= \sqrt{3k/4m}A = \sqrt{3}\pi fA
yosun
2005-11-01 02:14:55 |
fyi, add in dollar-sign wrappers around the equations in your comments... and the system processes your latex-compatible syntax into nifty-looking equations.
quote rreyes:
an alternative solution is conservation of energy
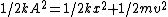
plugging in 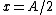 gives gives
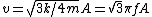
|
nitin
2006-11-16 13:32:49 |
Thumbs up mate!
|
|  |
|
|
Comments |
ethanque
2015-08-12 08:54:41 | Hooke's Law and Work Energy Theorem:
I couldn't remember my wave equations right away so I used the work energy theorem imagining this is a SHO/spring:
The particle has zero kinetic energy when 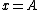 , and it is subject to the force , and it is subject to the force 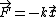 as it travels from as it travels from 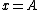 to to 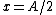 . i.e. the spring does work on the particle. . i.e. the spring does work on the particle.
So, integrate
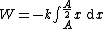
![\frac{1}{2} mv^2 = -k \frac{1}{2}[\frac{A^2}{4} - A^2]](/cgi-bin/mimetex.cgi?\frac{1}{2} mv^2 = -k \frac{1}{2}[\frac{A^2}{4} - A^2] )
Recall that 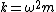 . Then . Then
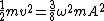
Recall that 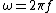 . Then . Then
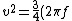^2 A^2 )
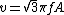 , which is option (B). , which is option (B).
Badda-bing badda-boom!
ethanque
2015-08-12 08:58:27 |
WOW! My solution looked fine in the preview. Sorry, for that jumbled mess of latex jargon... help?
|
yosun2015
2015-08-23 06:22:33 |
fixed! :)
|
|  | tpatt
2011-09-05 14:08:10 | Can someone explain why (omega*t + phi) = pi/6? I'm not following that step.
livieratos
2011-11-08 06:03:21 |
cause then sin(omega*t + phi) = sin(pi/6) = 1/2 as was given...
|
|  | anum
2010-11-11 11:37:29 | v=r*w =2*pi*f*A putting in A/2 in place of A gives v=pi*f* A . but its not correct; can anyone tell why?
IRFAN
2011-08-18 03:19:30 |
this velocity you have determin works only at particular point,in next you find the velocity of a different motion wich have halv the amplitrude
|
|  | shafatmubin
2009-11-02 10:17:59 | Simple Harmonic Motion flash card:
x = A cos (wt)
v = w Sqrt(A^2 - x^2)
a = -w^2 x
V = (1/2) k x^2 = (1/2) m w^2 x^2
T = (1/2) m v^2 = (1/2) m w^2 (A^2 - x^2) |  | wittensdog
2009-10-07 18:32:43 | Yet another solution...
You can easily find that the argument of the sine function must be 1/2. If you know the value of a sine function at one point, you immediately know the value of cosine, since,
cos^2 + sin^2 = 1 ==>
cos = sqrt ( 1 - sin^2 ) ==>
cos = sqrt(3) / 2
which then you just plug right into the velocity formula. It's similar to the original solution, but you don't need to remember what angles correspond to what values of sine and cosine. |  | lattes
2008-08-07 13:08:18 | Another to solve is: consider Let =A\cos{\omega t}) and and =-A\omega\sin{\omega t}) . Squaring both equation and summing them we get: . Squaring both equation and summing them we get: }^{2}+{(\frac{v}{A\omega})}^{2}=1) . Now let . Now let 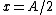 and solve for and solve for  . Thus . Thus 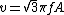 . (you should remember that . (you should remember that  !). A little bit longer solution, but it works. !). A little bit longer solution, but it works.
lattes
2008-08-07 13:09:33 |
"Another way to solve the problem is" ....
|
|  | rreyes
2005-10-31 08:06:24 | an alternative solution is conservation of energy
1/2kA^2=1/2kx^2+1/2mv^2
plugging in x=A/2 gives
v= \sqrt{3k/4m}A = \sqrt{3}\pi fA
yosun
2005-11-01 02:14:55 |
fyi, add in dollar-sign wrappers around the equations in your comments... and the system processes your latex-compatible syntax into nifty-looking equations.
quote rreyes:
an alternative solution is conservation of energy
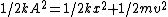
plugging in 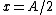 gives gives
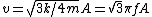
|
nitin
2006-11-16 13:32:49 |
Thumbs up mate!
|
zeper
2013-03-24 11:59:00 |
that is the best one....;)
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
