|
GR8677 #78
|
|
|
|
|
Alternate Solutions |
Saint_Oliver
2013-09-13 20:08:00 | 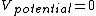
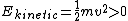 since since 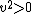
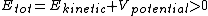
Therefore the total energy is greater than 0, which leaves only choice (C). |  |
|
|
Comments |
Saint_Oliver
2013-09-13 20:08:00 | 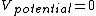
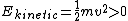 since since 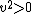
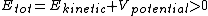
Therefore the total energy is greater than 0, which leaves only choice (C). |  | thebigshow500
2008-10-14 01:41:19 | So what will happen if radiation involves? I can't get a concise answer from this case. Anyone care to explain?
Poop Loops
2008-11-05 21:21:34 |
Makes things a lot harder. Charged particles radiate when they accelerate or decelerate. Things with mass accelerate or decelerate under a force. So they'd be pushing each other away and radiating, etc. So it's weird.
|
|  | grae313
2007-10-07 18:34:19 | Yosun, you assume the particle with a velocity is moving towards the stationary particle, but what if it was moving away from the particle? The answer must be valid for both cases (moving towards the particle, or away), and in the case where it moves away, potential energy will always be zero and the total energy will just be given by the positive kinetic energy. Thus, C is clearly the answer.
511mev
2009-11-05 21:57:33 |
I know this is an old comment, but i'd still like to clarify: the potential energy is only zero at time zero, but since the coulomb potential is conservative, then T + V = a constant (of unspecified sign, since we don't know the signs of the charges).
|
llama
2013-10-16 18:19:15 |
T+V is a positive constant, since initially V=0 (as stated in the question) and T>0 (since .5*mv^2>0)
|
|  | dbiggerstaff
2005-11-10 00:13:03 | There\'s a simpler way to look at it: the problem says that each particle initially has zero potential energy, but that one particle has a velocity relative to the other, which implies that it will have some kinetic energy in this reference frame. This means the total initial energy is T+U = (something)+0 = (something positive.) Since there\'s no radiation, energy will be conserved, and the total energy will remain (something positive.) Thus, the correct answer is (c).
nitin
2006-11-16 13:36:49 |
Thumbs up mate!
|
abc111
2009-10-02 02:54:55 |
can anyone explain... the sign cannot be determined unless intial velocity is known.....i am thinking...T is only thing that contains velocity here...but it will absorb minus sign because 1/2 m v^2 has a square term...
|
kaic
2013-10-09 13:37:53 |
It's highly unlikely that the particles would have negative energy, don't you think? While negative energy is not forbidden, and has been demonstrated to be possible, it's unlikely to show up on the GRE unless it is explicitly included as part of a question. As you said, the sign of the initial velocity does not matter because it is squared in the kinetic energy, so T is positive, and U is 0, so total energy E = T + V is positive.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
