|
GR0177 #89
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
tinytoon
2008-11-02 21:08:57 | This solution is incomplete because the initial moments of inertia cannot just be added like the solution says above. This is somewhat pedantic, since Yosun already got the right answer, but here it is nonetheless. The center of mass changes so you have to use:
)
This is the new center of mass and the moment of inertia now needs to be computed from this value. Now, the moment of inertia of the disk is:
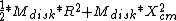
and the Moment of Inertia for the kid is:
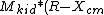^2)
Now you can add the two moments of inertia use conservation of momentum as detailed above.
GREview
2009-06-18 10:52:50 |
I think both the above comment ans Yosun's solutions are good to go. I used two different formulas for angular momentum 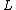 . .
First of all, but definition:
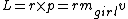
By hand-waiving, knowing that 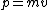 and and 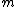 is analogous to is analogous to 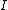 , the moment of inertia, and , the moment of inertia, and  is analogous to is analogous to  , then: , then:
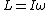
Now, for the girl I used the first one and with the merry-go-round, I used the second equation (and 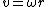 ): ):
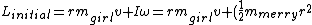\omega = r^2m_{girl}\omega+(\frac{1}{2}m_{merry}r^2)\omega)
This is what I think Yosun was getting at. The final angular momentum is just the moment of inertia of the merry-go-round rotating at a different angular velocity:
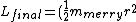\omega')
Setting the two equal obtains (E), or 2.8 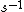 . .
|
kroner
2009-10-05 13:02:05 |
Considering the angular momentum around the center of mass is incorrect. The axis of rotation is fixed at the center of the disk because the merry-go-round is anchored to the ground there, so angular momentum is conserved with respect to that axis, NOT with respect to the center of mass as if the merry-go-round were floating out in space. Yosun's solution is correct.
|
walczyk
2012-10-30 15:25:43 |
You're missing a term for Ikid, by parallel axis theorem you need an extra Mkid*X^2 term
|
|  | gliese876d
2008-10-09 18:53:24 | I just have to say I love that the child is referred to as a "young padawan" in the solution!
kristen
2013-09-26 06:58:35 |
hahaha same!!
|
|  | medellin
2008-08-30 11:21:43 | I had thought that energy is conserved in this problem, so I got a different answer. I think that I now know the reason by the energy is not conserved, but I would like you give some comments about why the energy is not conserved.
blue_down_quark
2008-09-14 00:07:40 |
When the child starts moving and when he stops moving he should overcome friction which doesn't conserve the energy . In other words the kid is using part of the chemical energy stored in his muscles which should be accounted in the energy conservation equation .To make it more clear the kid is working on the system and that's why kinetic energy is increased in the final state. Note that this is because the center of the disk is fixed , so this is not a closed system (i.e. the work that the kid is doing on the disk is not equal to the work that the disk is doing on the kid , to cancel each other out . The latter is actually zero because the disk doesn't move)
|
edhopkins
2009-06-28 19:28:42 |
Actually the child will need to maintain friction not overcome it, or else he will discover quickly what the jedi mind force can do to his/her trajectory.
It seems to me that the original approach works because it is constrained motion (pin on the center of the large disk). Now what if it were say a section of the space station rotating in space with the child as an astronaut?
|
|  | OrbitGirl
2007-10-04 17:42:44 | The final equation is missing an angular velocity term in the numerator. As written, it comes out to be 1.4 rad/s. |  | nz_gre
2007-09-23 22:09:27 | Why isn't the mass of the child taken into account when calculating the final rotational inertia?
Since the child is now at the centre of the disk, isn't the mass used to calculate the final rotational inertia now 240 kg and not 200 kg as in this answer? It does end up giving a final  of 2.333 so is wrong but I'd still like a little explanation. of 2.333 so is wrong but I'd still like a little explanation.
tmearnest
2007-09-24 21:12:09 |
I suppose because children are point masses? If the child is a point mass, and it's at the center, then ^2 = 0) and it has no effect on the moment of inertia. and it has no effect on the moment of inertia.
|
Furious
2007-10-22 17:37:00 |
The childs inertia is still taken into account. The initial Inertias are the inertia of the disk, 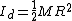 plus the inertia of the child, plus the inertia of the child,  where d is the distance from the point of rotation to the child. Now let's think about this children, what is d when the child is at the center of the merry-go-round? where d is the distance from the point of rotation to the child. Now let's think about this children, what is d when the child is at the center of the merry-go-round?
|
Furious
2007-10-22 17:37:42 |
Crap, I totally didn't see that first comment.
|
insertphyspun
2011-02-21 11:02:32 |
Using 240kg would be correct if the mass of the child were evenly distributed over the surface area of the disk. The problem could be changed to say consider a snowman at the edge of the disk. The disk is stopped, the snowman melts, then refreezes, and the disk is given the same angular impulse. Now what is  ? (If he melts while the disk is spinning, he flies off). ? (If he melts while the disk is spinning, he flies off).
|
yummyhat
2017-10-27 04:04:50 |
omg physpun
|
yummyhat
2017-10-27 04:08:14 |
what if the kid just melts and his goo sticks to the disc
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
