|
GR0177 #47
|
|
|
|
|
Alternate Solutions |
physgre
2015-10-15 07:46:53 | 原答案不对,是绝热自由膨胀而不是等温过程。无功,无热,无能变,有熵变。可参考travis.nicholson的答案。 |  | anmuhich
2009-03-14 14:25:27 | Another way, similar to Scottopoly's and much faster than the others.
S= ln (states)
The number of states is proportional to V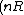) . If you think about it this makes sense that for every little portion of volume you can stick a molecule in it, assuming the molecule takes up negligable space. . If you think about it this makes sense that for every little portion of volume you can stick a molecule in it, assuming the molecule takes up negligable space.
change in S = ln (2V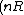) ) - ln(V ) - ln(V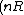) ) )
If you manipulate the logs it works out nicely. There may be a few scaling factors I'm missing in this solution but it works for getting the answer and that's all that matters on the GRE. |  | eliasds
2008-09-20 20:46:57 | The solution that Yosun gave is almost completely correct. The only problem is the incomplete way we found dW. You can't take the derivative of 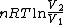 because the term is a constant (i.e. derivative is zero). Here is how you find dQ: because the term is a constant (i.e. derivative is zero). Here is how you find dQ:
Since we are looking for 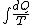 and this is an isothermal process Q=W and this is an isothermal process Q=W 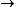 dQ=dW dQ=dW
We have to leave dQ in it's integral form. So we get:
Q = 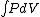 = = 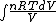
and the derivative of an integral is the original function.
dQ = 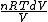
S = 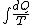 = = 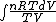 = = 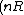ln \frac{V_2}{V_1}) = = 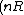ln2)
|  | scottopoly
2006-10-29 22:56:06 | Here's how I solved it quickly:
entropy is the log of the number of free states. For EACH molecule, the number of free states goes up by a factor of 2. There are thus 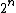 times more states. times more states. =n\ \ln(2)) . Throw in some normalization R to deal with moles. . Throw in some normalization R to deal with moles. |  | travis.nicholson
2006-10-23 02:18:52 | A more appropriate solution would be:
Since there is no work being done on or by the gas, the energy of the gas remains constant. Also, since the change in volume of the gas is a discontinuous process, it would be a difficult task to compute the entropy change via a direct analysis of free expansion.
However, since entropy is a state variable, the entropy change will be the same if the gas had expanded adiabatically and quasistatically (i.e., if the "impenetrable wall" were the face of a piston that slowly moved until the gas expanded) and without a change in energy rather than through free expansion.
The former case can be analyzed with the first law of thermodynamics:
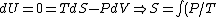 dV)
Using the ideal gas law, 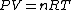 , , 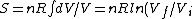 = n R ln(2)) |  |
|
|
Comments |
physgre
2015-10-15 07:46:53 | 原答案不对,是绝热自由膨胀而不是等温过程。无功,无热,无能变,有熵变。可参考travis.nicholson的答案。
ä¸è®²ççè¾
2019-04-03 00:18:43 |
èå¥ï¼ç¨³ï¼æ就说insulatoråªæ¥çQ\r\n
|
|  | amber
2014-10-22 22:14:44 | Variation of these problem to keep in mind:
If both volumes start out with the same particle and the partition is removed, the change in entropy is zero. |  | amber
2014-10-22 22:09:14 | one can easily eliminate D and E because the change in entropy can't ever be less than zero |  | ffddff
2009-10-04 11:33:59 | When the wall is SUDDENLY remoed, you CANNOT use quasistaic approximation, I guess, and $kTdS>\delta Q (=0 here)$. So I guess only way is to use the fact that entropy is the log of the number of free states. And I guess anmuhich scottopoly are right.
kroner
2009-10-05 20:40:08 |
You are right that the process is different, but the final state of the gas is exactly the same, which means the change in entropy is the same as if it underwent the equivalent quasistatic process. Entropy, being a thermodynamic potential, doesn't care how you get there.
|
|  | anmuhich
2009-03-14 14:25:27 | Another way, similar to Scottopoly's and much faster than the others.
S= ln (states)
The number of states is proportional to V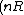) . If you think about it this makes sense that for every little portion of volume you can stick a molecule in it, assuming the molecule takes up negligable space. . If you think about it this makes sense that for every little portion of volume you can stick a molecule in it, assuming the molecule takes up negligable space.
change in S = ln (2V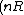) ) - ln(V ) - ln(V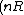) ) )
If you manipulate the logs it works out nicely. There may be a few scaling factors I'm missing in this solution but it works for getting the answer and that's all that matters on the GRE.
kroner
2009-10-05 12:05:16 |
More accurately, the number of states for each molecule is proportional to the volume, call the number 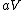 where where  is some arbitrary constant. The number of states for is some arbitrary constant. The number of states for 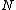 molecules is then molecules is then ^N) . .
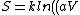^N) = Nk ln(aV) = nR ln(aV))
When the volume doubles,
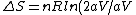 = nR ln2)
|
aolla2001
2010-03-21 06:40:33 |
Why we assume the process is isothermal? It says the container is thermally isolated, that means no heat is exchanged and the process is adiabatic.
|
busy3
2011-11-07 11:29:48 |
Is there anything wrong with thinking about the problem like this:
If there was 1 particle Sf=k*ln(states) and states = 2 and Si = k*ln(1) = 0
**states: particle in left or right
multiply by the amount of particles get Sf=N*kln(2)
Nk=nR ->Sf=n*R*ln(2)
?
|
|  | isentropic
2008-10-17 20:13:02 | isn't the simplest way to go about this to use the entropy for an ideal gas.
in this case we have S=Nkln(V_f/V_i).
we know Nk=nR and V_f=2V_i
so we end up with S=nRln(2V_i/V_i) which equals S=nRln2 (B) |  | eliasds
2008-09-20 20:46:57 | The solution that Yosun gave is almost completely correct. The only problem is the incomplete way we found dW. You can't take the derivative of 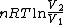 because the term is a constant (i.e. derivative is zero). Here is how you find dQ: because the term is a constant (i.e. derivative is zero). Here is how you find dQ:
Since we are looking for 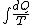 and this is an isothermal process Q=W and this is an isothermal process Q=W 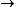 dQ=dW dQ=dW
We have to leave dQ in it's integral form. So we get:
Q = 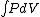 = = 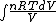
and the derivative of an integral is the original function.
dQ = 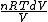
S = 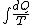 = = 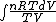 = = 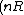ln \frac{V_2}{V_1}) = = 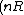ln2)
|  | Imperate
2008-08-30 14:34:41 | I find the most logical way to think about this problem, is to start with the fact the system is thermally insulated, this 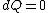 (i.e. it is adiabatic). However this does not imply that the entropy change is zero, because (i.e. it is adiabatic). However this does not imply that the entropy change is zero, because 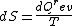 only applies when only applies when 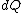 refers to the heat exchanged in a reversible process. This is free expansion and thus a spontaneous process, all spontaneous changes are irreversible (non quasi static). For a process to be "isentropic" (i.e. constant in entropy) it must be both reversible (quasistatic) AND adiabatic ( refers to the heat exchanged in a reversible process. This is free expansion and thus a spontaneous process, all spontaneous changes are irreversible (non quasi static). For a process to be "isentropic" (i.e. constant in entropy) it must be both reversible (quasistatic) AND adiabatic ( 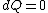 ). So we definitely can say there will be a change in entropy. ). So we definitely can say there will be a change in entropy.
The actual process is adiabatic so 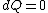 , and the expansion is also free implying the gas does no work in expanding. Now since , and the expansion is also free implying the gas does no work in expanding. Now since 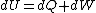 , we see if no heat is exchanged and no work done, the energy change of the gas must also be zero. For an ideal gas , we see if no heat is exchanged and no work done, the energy change of the gas must also be zero. For an ideal gas  ) only, implying if E is constant so is the temperature. So now we know the initial and final states have equal temperature, T. only, implying if E is constant so is the temperature. So now we know the initial and final states have equal temperature, T.
Entropy is a state variable, so it doesn't matter which process we look at to go from the initial state to final state, as long as the initial/final states are the same as for the actual process. So we can choose the most conveinient process to work out the entropy change.
Since the temperate is constant, it makes sense to evaluate the entropy change by looking at the corresponding quasi-static isothermal process (picture the gas surrounded by a heat bath at constant temp, T, and doing work by quasistatically pushing against a piston held in place by atmospheric air of pressure only infinitessimally lower than the gas ideal gas inside).
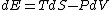 Since the gas is still ideal, and the temperature fixed =>dE=0. This leads to the relation Since the gas is still ideal, and the temperature fixed =>dE=0. This leads to the relation 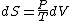 . Now simply using the ideal gas law . Now simply using the ideal gas law 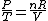 and subbing in; and subbing in;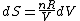 => => 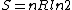 . Choice B . Choice B
The actual process is adiabatic so [tex]dQ=0 [/tex], and the expansion is also free implying the gas does no work in expanding. Now since [tex]dU=dQ+dW [/tex], we see if no heat is exchanged and no work done, the energy change of the gas must also be zero. For an ideal gas [tex] E=E(T) [/tex] only, implying if E is constant so is the temperature. So now we know the initial and final states have equal temperature, T.
Entropy is a state variable, so it doesn't matter which process we look at to go from the initial state to final state, as long as the initial/final states are the same as for the actual process. So we can choose the most conveinient process to work out the entropy change.
Since the temperate is constant, it makes sense to evaluate the entropy change by looking at the corresponding quasi-static isothermal process (picture the gas surrounded by a heat bath at constant temp, T, and doing work by quasistatically pushing against a piston held in place by atmospheric air of pressure only infinitessimally lower than the gas ideal gas inside).
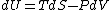 Since the gas is still ideal, and the temperature fixed =>dU=0. This leads to the relation Since the gas is still ideal, and the temperature fixed =>dU=0. This leads to the relation 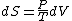 . Now simply using the ideal gas law . Now simply using the ideal gas law 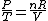 and subbing in; and subbing in;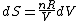 => => 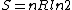 .Choice B .Choice B
PhyAnnie
2008-11-02 01:05:41 |
Thank you very much, very clear and logic... the best explanation I ever see! :-)
|
|  | Furious
2007-10-20 15:38:10 | I totally know Travis Nicholson in real life...his solution is awesome. |  | kostas_zarganis
2007-01-15 18:10:41 | The solution is a bit compicated. The problem says thermally insulated which means no tranfer of energy (Q = 0). So one can think no Q so no change in entropy...
The trick is that we hypotize (because the entropy really changes while the volume comes bigger so the mess of molecules has gone up) that we have a reversible process (we must mention it because of this we can calculate anything from the known equations)in which the T is constant (isothermal process). The others is already written...
xxxxnguyen
2008-08-29 16:38:07 |
If no heat transfer (Q = 0), then dU = dW so T can't be constant?
How can it be isothermal and adiabatic at the same time?
|
|  | RootMeanSquare
2006-11-19 02:41:06 | Maybe to clear the confusion a little: thermally insulated means dQ = 0, and hence generally adiabatic (or isentrop, which I think is a way nicer word:-)). However, we aren't talking about any cyclic processes here, the gas doesn't have to do any work, and hence it is correct here to say this process is both isentrop and isotherm. Maybe Yosun could point out that the Work calculated would be done by a _reversible_ process going from one state to the other. This work lost to the irreversibility is the equivalent to the entropy created.
Scottopoly: Nice solution, your 'normalisation' R is just your n times 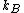 which you forgot in your definition which you forgot in your definition |  | scottopoly
2006-10-29 22:56:06 | Here's how I solved it quickly:
entropy is the log of the number of free states. For EACH molecule, the number of free states goes up by a factor of 2. There are thus 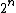 times more states. times more states. =n\ \ln(2)) . Throw in some normalization R to deal with moles. . Throw in some normalization R to deal with moles.
casaubon
2008-10-07 09:30:31 |
awesome.
|
|  | travis.nicholson
2006-10-23 02:18:52 | A more appropriate solution would be:
Since there is no work being done on or by the gas, the energy of the gas remains constant. Also, since the change in volume of the gas is a discontinuous process, it would be a difficult task to compute the entropy change via a direct analysis of free expansion.
However, since entropy is a state variable, the entropy change will be the same if the gas had expanded adiabatically and quasistatically (i.e., if the "impenetrable wall" were the face of a piston that slowly moved until the gas expanded) and without a change in energy rather than through free expansion.
The former case can be analyzed with the first law of thermodynamics:
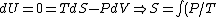 dV)
Using the ideal gas law, 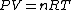 , , 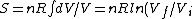 = n R ln(2))
Imperate
2008-08-30 14:46:42 |
you mean the same as if the gas had expanded isothermally and quasistatically, instead of adiabatically and quasistatically , right?
If we looked at the process were the gas expanded adiabatically and quasistatically, then 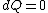 , and the gas does work pushing out the piston (reversibly now so that PdV applies, so not free expansion), thus the energy (and consequently for an ideal gas, the temperature, decreases). So an adiabatic and quasistatic process, would not take us from the initial state to final state, that the actual process would. (i.e with , and the gas does work pushing out the piston (reversibly now so that PdV applies, so not free expansion), thus the energy (and consequently for an ideal gas, the temperature, decreases). So an adiabatic and quasistatic process, would not take us from the initial state to final state, that the actual process would. (i.e with 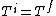 ) )
The equivalent process must be an isothermal and quasistatic one, since the final state of the ACTUAL process has the same temperature as the initial state.
|
luwei0917
2014-03-29 12:36:19 |
this solution is good
|
Ithillhoss
2015-10-22 03:53:25 |
This is the correct one, the free expansion cannot be treated as the quasistatic process!
|
|  | travis.nicholson
2006-10-23 01:57:05 | The expression for 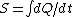 is true only for an isothermal process, and free expansion is not isothermal. is true only for an isothermal process, and free expansion is not isothermal. |  | backyard
2006-10-10 19:30:01 | How did you know it's an isothermal process?
kevglynn
2006-11-03 08:47:21 |
It says in the first sentence, "a sealed and 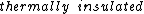 container," which I took to mean isothermal, i.e., no temperature change. container," which I took to mean isothermal, i.e., no temperature change.
|
wangjj0120
2008-10-27 09:47:20 |
kevglynn: Doesn't "a sealed and thermally insulated container" mean adiabatic ?
|
|  | tsak
2006-09-23 00:27:07 | The solution given by the ETS in it´s solutions, is -2nRln2. I find your answer to be correct as well however I am troubled.
herrphysik
2006-09-27 00:30:06 |
tsak: Where did you get ETS solutions from? If you just mean the answer key, then they do give the correct answer (B)...you may have looked at the previous problem which had answer (E), which is 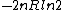 in this problem. in this problem.
The answer here cannot possibly be negative (decreasing entropy), since the only change to the system is an increase in volume, i.e. increase in number of available states and thus entropy.
|
|  | tsak
2006-09-23 00:25:27 | |  | vbphysics
2005-12-09 09:48:35 | the first line should read
) = = 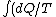) |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
