|
GR0177 #46
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }de Broglie Wavelength }de Broglie Wavelength
Since ) and the de Broglie wavelength gives and the de Broglie wavelength gives 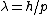 , one can find the initial wavelength , one can find the initial wavelength 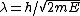 . This yields an expression for . This yields an expression for 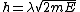
When the particle enters the well, its energy becomes 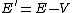 , and thus , and thus }) . .
Plugging h in, one has }) , which is choice (E). , which is choice (E).
(This above solution is due to the lout Marko.)
Also, the current author's original approach leads to the right result, but it hand-waves the massiveness of the particle:
The initial kinetic energy of the free particle is its total energy 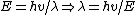 . But, since one's dealing with de Broglie, one has . But, since one's dealing with de Broglie, one has 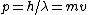 . Thus, . Thus, ) . .
In the potential, its energy becomes  . Replace E above with that to get . Replace E above with that to get )) . But, from the same relation above, one has . But, from the same relation above, one has 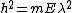 . Thus, . Thus,  = \lambda^2 (1-V/E)^-1) . This is choice (E). . This is choice (E).
|
|
|
Alternate Solutions |
greatspirits
2012-11-04 20:01:38 | Ok,..think I finally figured this one out, partially due to the posted comments solutions, so thanks. However, I now see a path which seems less cloudy: the wave equation is 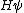 = =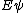 , with the classical hamiltonian being , with the classical hamiltonian being 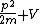 . Naturally then . Naturally then 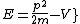 Debroglie theory states Debroglie theory states 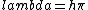 . So ommiting cancelling factors . So ommiting cancelling factors 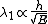 , while , while 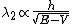 . The problem asks for the new wavelength in terms of the old one. This is . The problem asks for the new wavelength in terms of the old one. This is ) or or 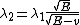 which crunches down to choice E. which crunches down to choice E.
greatspirits
2012-11-04 20:05:21 |
the above should read "Debroglie theory states 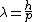 . So..." . So..."
|
|  | phoxdie
2010-11-12 22:25:35 | I think limits work fine in this problem, but please let me know if my reasoning is wrong. First consider if V=0 we should have the same wavelength as we did before, this eliminates choices A and C. Next we could consider V as it goes to  , in this case with the remaining solutions, , in this case with the remaining solutions,  either goes to either goes to  as in B or D or it goes to zero as in E. Of these choices only E makes sense as the de Broglie wavelength should never be infinite (I am pretty sure about that). But please if something is wrong with this reasoning say something. as in B or D or it goes to zero as in E. Of these choices only E makes sense as the de Broglie wavelength should never be infinite (I am pretty sure about that). But please if something is wrong with this reasoning say something. |  | BerkeleyEric
2010-07-17 17:13:11 | I think the quickest way to do this one is to look at 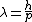 and and  and realize that there must be some sort of power of 2 or 1/2. This eliminates all but (D) and (E). and realize that there must be some sort of power of 2 or 1/2. This eliminates all but (D) and (E).
Then (if there is enough time), one can consider that the wavelength should increase so only (E) works. |  | Jeremy
2007-09-20 17:40:02 | The great thing about the Physics GRE is that eliminating the 4 wrong answers is just as good as picking the 1 right answer ;) This means you may be able to pick the right answer without solving (or even knowing how to solve) the problem. When recognized right away, this is often the fastest method of solution... Here's how to eliminate the four wrong answers on this problem:
Think of extreme, special, or limiting cases, like when V > E. This is corresponds to a classically forbidden region, i.e. a region of exponential decay for the wave function. Therefore, 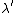 cannot be real, IT MUST BE COMPLEX. This eliminates everything but (E). cannot be real, IT MUST BE COMPLEX. This eliminates everything but (E).
These kinds of elimination arguments can often seem flimsy, but this one comes straight from the equations...
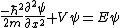
becomes
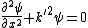 , ,
with
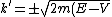}/\hbar) . .
The solution has the form of a complex exponential (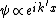 ), so we see that ), so we see that 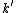 is actually the wave vector ( is actually the wave vector (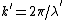 ). V > E means ). V > E means 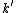 , and therefore , and therefore 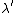 , is imaginary. Of course, you don't really need to work with the differential equation, remembering the "classically forbidden region" part would be good enough for solving the problem. , is imaginary. Of course, you don't really need to work with the differential equation, remembering the "classically forbidden region" part would be good enough for solving the problem. |  |
|
|
Comments |
BruceLyu
2018-10-24 07:35:28 | This problem involves two plane waves (de-Broglie waves) in two regions. Initially, it is  and after entering the region with potential energy V, the kinetic energy becomes and after entering the region with potential energy V, the kinetic energy becomes 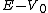 and the corresponding wave is and the corresponding wave is 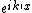 . For a plane wave, the energy is . For a plane wave, the energy is 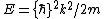 so \r\n so \r\n^2 = \\frac{E}{E-V_0} = (\\frac{\\lambda\'}{\\lambda})^2) \r\nand solve it we get the final answer E. \r\nand solve it we get the final answer E. |  | mgilbardaji
2018-03-17 16:42:15 | Before speaking of de Broglie\'s wavelengths, we can compute the change in the momentum of the particle. The initial energy is 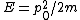 and when the particle enters the other region, the total energy doesn\'t change (the kinetic term, hence the momentum, will change) and we\'ll have and when the particle enters the other region, the total energy doesn\'t change (the kinetic term, hence the momentum, will change) and we\'ll have 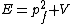 . From those two formulas we can easily get . From those two formulas we can easily get ) . Finally, we only need to remember that . Finally, we only need to remember that 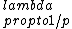 and then the wavelength and then the wavelength ^{-1/2}) as E says. as E says. |  | collectedsoul
2016-08-10 15:11:12 | If I use \\lambda = hc/E and replace with \\lambda = hc/(E-V) I don\'t get the right answer, why is this? |  | greatspirits
2012-11-04 20:01:38 | Ok,..think I finally figured this one out, partially due to the posted comments solutions, so thanks. However, I now see a path which seems less cloudy: the wave equation is 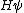 = =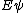 , with the classical hamiltonian being , with the classical hamiltonian being 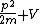 . Naturally then . Naturally then 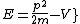 Debroglie theory states Debroglie theory states 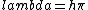 . So ommiting cancelling factors . So ommiting cancelling factors 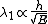 , while , while 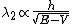 . The problem asks for the new wavelength in terms of the old one. This is . The problem asks for the new wavelength in terms of the old one. This is ) or or 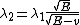 which crunches down to choice E. which crunches down to choice E.
greatspirits
2012-11-04 20:05:21 |
the above should read "Debroglie theory states 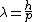 . So..." . So..."
|
|  | dr104
2011-08-26 18:24:09 | None of this really makes sense to me.
I get the way it is being done, however the question just seems flawed. Please tell me if I am wrong.
First if I just think intuitively I would think the new wavelength is the same as the old one because 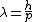 and as soon as the particle enters a new potential, it's momentum is not going to change! Not unless you wait for some time, but the problem doesn't say that... and as soon as the particle enters a new potential, it's momentum is not going to change! Not unless you wait for some time, but the problem doesn't say that...
Also it seems that they did E' wrong... Wouldn't the new total energy be E'=E+V so that E=E'-V ? They said E'=E-V which implies that E=E'+V so now E is the total energy again, but they already defined E as the original energy, when we enter a region with a completely different potential the total energy should change, so this whole question seems messed up to me, and so does the solution...
Am I the only one?
Am I wrong?
Please tell me what I am thinking incorrectly |  | phoxdie
2010-11-12 22:25:35 | I think limits work fine in this problem, but please let me know if my reasoning is wrong. First consider if V=0 we should have the same wavelength as we did before, this eliminates choices A and C. Next we could consider V as it goes to  , in this case with the remaining solutions, , in this case with the remaining solutions,  either goes to either goes to  as in B or D or it goes to zero as in E. Of these choices only E makes sense as the de Broglie wavelength should never be infinite (I am pretty sure about that). But please if something is wrong with this reasoning say something. as in B or D or it goes to zero as in E. Of these choices only E makes sense as the de Broglie wavelength should never be infinite (I am pretty sure about that). But please if something is wrong with this reasoning say something. |  | BerkeleyEric
2010-07-17 17:13:11 | I think the quickest way to do this one is to look at 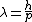 and and  and realize that there must be some sort of power of 2 or 1/2. This eliminates all but (D) and (E). and realize that there must be some sort of power of 2 or 1/2. This eliminates all but (D) and (E).
Then (if there is enough time), one can consider that the wavelength should increase so only (E) works. |  | tau1777
2008-11-03 18:51:04 | i had been having a tough time with this problem and i finally just got, i used that the initial one is ) . then going into a potential the energy increases to E+V. Then the new lambda is . then going into a potential the energy increases to E+V. Then the new lambda is ) . Then I just thought of what I would have to multiply the first equation with to get the second one with the V. . Then I just thought of what I would have to multiply the first equation with to get the second one with the V.
After finally getting it I see that (E) is the only choice that lists $\lambda4 to the -1/2 power. this should have given the problem away at the very beginning i can't believe i never realized this before.
i guess the only issue with my solution is that I don't get that minus sign in (E) and i guess that's because the problem wants you to assume that the particle fell into some sort of potential well, instead of lets say a repulsive potential. vagueness of the ETS at its best.
hope this helps someone.
sonnb
2008-11-08 19:58:35 |
The free particle has an inital total energy of E, which is equal to its kinetic energy. When it enters the region of potential energy V, its total energy remains the same (by conservation of energy) so that its new kinetic energy is E-V.
|
|  | Poop Loops
2008-11-01 16:47:16 | So how come I can't use ^2 + (mc^2)^2) and then ignore and then ignore 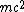 ? ?
CarlBrannen
2010-10-05 21:20:12 |
The answer given above is wrong in that kinetic energy is given by 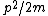 only in the non relativistic limit. But they don't mention "non relativistic" in the problem. only in the non relativistic limit. But they don't mention "non relativistic" in the problem.
If you use 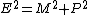 , you find that you get: , you find that you get:
^{-1/2}\sqrt{E+2m}/\sqrt{E+2m-V}) . .
This is equivalent to the GRE answer only in the non relativistic limit (i.e. where m >> E,V).
I think that the problem is faulty at best. I left it unanswered when I took the practice exam, now I feel better about it.
|
|  | gre..
2007-10-24 06:06:45 | err.. E = 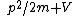 and and 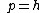 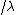 (from (from 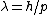 ) p -> E then ) p -> E then  = = }) now solve the prob, when V=0 now solve the prob, when V=0  = = 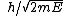 and for V : not zero the new wavelength and for V : not zero the new wavelength 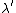 is is 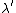 = = }) = ( = (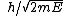 )/( )/( ) = ) = 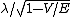 (E). (E). |  | gre..
2007-10-24 06:02:40 | err.. rnE = 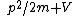 and and 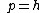 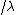 (from (from 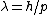 )rnrnp -> Ernrnthenrn )rnrnp -> Ernrnthenrn = = }) rnrnrnrnnow solve the prob,rnwhen V=0rn rnrnrnrnnow solve the prob,rnwhen V=0rn = = 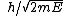 rnrnand for V : not zerornthe new wavelength rnrnand for V : not zerornthe new wavelength 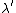 isrn isrn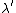 = = }) = ( = (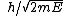 )/( )/( )rn = )rn = 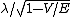 rnrn(E). rnrn(E). |  | Jeremy
2007-09-20 17:40:02 | The great thing about the Physics GRE is that eliminating the 4 wrong answers is just as good as picking the 1 right answer ;) This means you may be able to pick the right answer without solving (or even knowing how to solve) the problem. When recognized right away, this is often the fastest method of solution... Here's how to eliminate the four wrong answers on this problem:
Think of extreme, special, or limiting cases, like when V > E. This is corresponds to a classically forbidden region, i.e. a region of exponential decay for the wave function. Therefore, 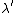 cannot be real, IT MUST BE COMPLEX. This eliminates everything but (E). cannot be real, IT MUST BE COMPLEX. This eliminates everything but (E).
These kinds of elimination arguments can often seem flimsy, but this one comes straight from the equations...
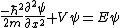
becomes
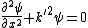 , ,
with
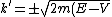}/\hbar) . .
The solution has the form of a complex exponential (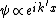 ), so we see that ), so we see that 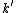 is actually the wave vector ( is actually the wave vector (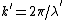 ). V > E means ). V > E means 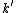 , and therefore , and therefore 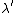 , is imaginary. Of course, you don't really need to work with the differential equation, remembering the "classically forbidden region" part would be good enough for solving the problem. , is imaginary. Of course, you don't really need to work with the differential equation, remembering the "classically forbidden region" part would be good enough for solving the problem. |  | Jeremy
2007-09-20 16:14:51 | To clarify: The snake in the grass with 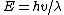 is that here is that here  represents the phase velocity (wave velocity), which is not always the same as the group velocity (particle velocity). However, this is what is being assumed in the originally posted solution. In equations: represents the phase velocity (wave velocity), which is not always the same as the group velocity (particle velocity). However, this is what is being assumed in the originally posted solution. In equations:
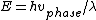 and and 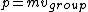 , ,
so the original solution implicitly - and erroneously - uses 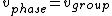 . In general, the two are not equal because . In general, the two are not equal because
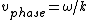 , ,
whereas
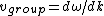 . .
For a plane wave solution in free space, the dispersion relation is: 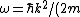) , so in fact, , so in fact, 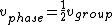 . This explains the difference of a factor of 2 in the two solutions' equation for . This explains the difference of a factor of 2 in the two solutions' equation for  ; one (correctly) has ; one (correctly) has 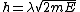 , while the original version has , while the original version has ) . The error of equating the two velocities happens twice (once for . The error of equating the two velocities happens twice (once for  , and once for , and once for 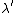 ) and cancels in division in the algebra to solve the problem. This is why the first approach still gets the right answer. ) and cancels in division in the algebra to solve the problem. This is why the first approach still gets the right answer. |  | joshuacc1
2005-12-03 15:01:42 | marko,
The question said a free particle with initial kinetic energy E. A free particle doesn't necessarily need to be a photon. Besides, a de broglie wave is calculated from a particle with a mass. |  | Marko
2005-11-11 13:43:35 | This derivation here gives the correct result (E) but is fundumentally flawed. E is not hv/\lambda. That for a photon with no mass. In this problem E=p^{2}/2m as always. Indeed \lambda=h/p and it follows from these two CORRECT statements that indeed the answer is E. Who ever did it the other was nothing more but a lucky son-of-a-bitch.
yosun
2005-11-11 13:58:27 |
-.- daughter of a bitch. btw marko, the bitch suggests that you put dollar-sign wrappers around your equations so that you get 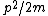 instead of p^2/2m. your solution has been added above. instead of p^2/2m. your solution has been added above.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
