|
GR0177 #33
|
|
|
|
|
Alternate Solutions |
danielkwalsh
2010-09-05 18:25:18 | A quick trick: the equation 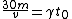 is correct, but for an extremely relativistic particle, as we clearly have here, the decay time in the lab frame can be well approximated as is correct, but for an extremely relativistic particle, as we clearly have here, the decay time in the lab frame can be well approximated as 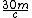 , since , since  . This simplifies the math a lot more in solving for . This simplifies the math a lot more in solving for  . This gives . This gives  , which is closest to choice (D). , which is closest to choice (D). |  | Herminso
2009-09-21 13:42:50 | Use 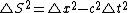 . In the own rest frame of the pion . In the own rest frame of the pion 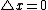 , and thus: , and thus:
^2=-9) . .
But in the Lab frame,
^2-c^2\triangle t'^2) . .
Now, using the invariant 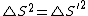 , ,
^2-c^2\triangle t'^2=-9)  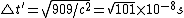
Thus, 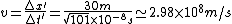 . .
ramparts
2009-10-07 13:32:13 |
By far the best solution, because it's the most elegant and because it makes the algebra significantly easier without a calculator.
|
|  |
|
|
Comments |
danielkwalsh
2010-09-05 18:25:18 | A quick trick: the equation 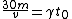 is correct, but for an extremely relativistic particle, as we clearly have here, the decay time in the lab frame can be well approximated as is correct, but for an extremely relativistic particle, as we clearly have here, the decay time in the lab frame can be well approximated as 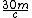 , since , since 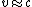 . This simplifies the math a lot more in solving for . This simplifies the math a lot more in solving for  . This gives . This gives  , which is closest to choice (D). , which is closest to choice (D). |  | Herminso
2009-09-21 13:42:50 | Use 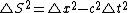 . In the own rest frame of the pion . In the own rest frame of the pion 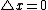 , and thus: , and thus:
^2=-9) . .
But in the Lab frame,
^2-c^2\triangle t'^2) . .
Now, using the invariant 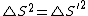 , ,
^2-c^2\triangle t'^2=-9)  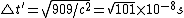
Thus, 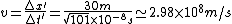 . .
hanin
2009-10-04 22:13:57 |
Why  ? ?
|
kroner
2009-10-05 11:36:41 |
The pion's own rest frame is the frame where it doesn't move so 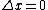 . .
|
ramparts
2009-10-07 13:32:13 |
By far the best solution, because it's the most elegant and because it makes the algebra significantly easier without a calculator.
|
|  | Ning Bao
2008-02-01 06:26:28 | Pions don't reach speed of light (incidentally, this eliminates E). It must be going very close, however, to contract 30m to a little less than 3 meters to not violate this. This means D.
noether
2009-11-05 15:28:05 |
If 2.99*10^8 were listed as an answer, would you have chosen that?
|
gravity
2010-11-10 00:37:22 |
Yeah. This one was tricky. I did most of what everybody else did and ended with 30 c/(909)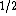 which I figured looked more like more like c than it did 2.98 x 10^8. which I figured looked more like more like c than it did 2.98 x 10^8.
Gah. I should have known better! At least it's not the real test.
|
|  | StrangeQuark
2007-05-12 12:03:43 | To make this faster (avoid the "messy" fraction)
Note to start that this is not a photon thus answer E is out.
now as above,
L=v 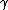 t t
L 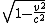 =v t =v t
some simplification steps
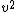 = =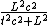
now plug and chug...
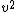 = =^2 ((3)(10^8)(\frac{m}{s}))^2}{(10^{-8}s)^2 ((3)(10^8)(\frac{m}{s}))^2+(30m)^2})
Note now that we have a
(10^{8}))
in the first term in the denominator, leaving only
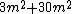
in the denominator,
but 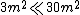
so we simplify
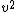 < <^2 ((3)(10^8)(\frac{m}{s}))^2}{(30m)^2})
after canceling we see that
v<(10^8)\frac{m}{s})
but only by a very small amount thus we have D |  | boundforthefloor
2006-11-26 05:25:22 | Can anyone clarify this? I'm befuddled and can't find much that helps.
johnyp03
2006-11-29 17:48:43 |
So, you know L=30=vt in the lab frame. But, in the pion's frame, there is time dilation. So, t=t'=(gamma)t0 where t0=3*10^-8, gamma=1/(sqrt(1-v^2/c^2)). So:
30 = v(gamma)t0 = v*(10^-8)/(sqrt(1-v^2/c^2))
30*sqrt(1-v^2/c^2) = v*(10^-8)
900*(1-v^2/c^2) = v^2(10^-16)
900 = v^2*10^-16 + v^2*900/c^2
==================> 900/c^2=(900/9)*10^-16=10^-14
900 = v^2(10^-16 + 10^-14)
sqrt(900/(10^-16+10^-14)) = v
30/sqrt(1.01*10^-14) = v
30/1.005*10^-7 = v
v ~ 2.98*10^8
Hope this helps
|
boundforthefloor
2006-12-01 11:40:08 |
Thanks johnyp. The actual equation setup was killing me, now that I've seen the calcualtions it makes much more sense.
|
VanishingHitchwriter
2006-12-01 14:07:02 |
Surround your expressions with dollar signs for latex equations. Here's the guy's comment back again...
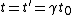 where where 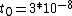 , , ) . So: . So:
/(\sqrt{1-v^2/c^2}))
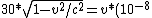)
 = v^2(10^{-16}))
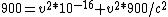
==================> 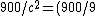*10^{-16}=10^{-14})
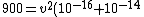)
) = v)
 = v)
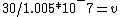
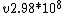
|
matweiss
2010-09-29 09:31:49 |
hey, I don't understand why t0 is 3 x 10^-8. it seems like I thought t in the frame of the particle was 10^-8 s and that (if you assume the particle to essentially be moving at light speed) then t in the lab frame equals 30/c= 1x 10^-7. any help?
|
|  | senatez
2006-11-02 12:46:13 | I ended up with a messy fraction 10c/10.1 which you estimate as .99c. This is about 2.98*10^8. I sure wish they would give easier arithmatic, it is waists a lot of time. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
