|
GR0177 #34
|
|
|
|
|
Alternate Solutions |
thebigshow500
2008-10-12 16:10:18 | Just Check out Griffiths p.502 - "The invariant interval." Everything is super clear there.
Mr. Griffiths derives the result of interval between two events as I = 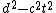
I < 0 refers to timelike interval. Two events occur simultaneously.
I > 0 refers to spacelike interval. Two events occur at the same place.
I = 0 refers to lightike interval. Two events are connected by a signal traveling at c!
For this question, I > 0, so the term 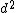 dominates dominates 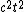 . One can deduct the answer (C)!! . One can deduct the answer (C)!!
|  | ivalmian
2008-03-25 19:02:24 | You can also show this through a little math.
We know that for 2 arbitrary reference frames  and and  , the time intervals between the two events is: , the time intervals between the two events is:
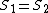
Plugging in  , , 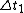 , , 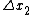 , and , and 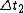 we get: we get:
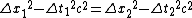
If in 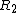 the event is perceived as simultaneous, then the event is perceived as simultaneous, then 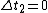 . Thus we get: . Thus we get:

Dividing by 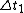 we get: we get:
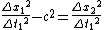
Adding 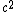 to both sides we get: to both sides we get:
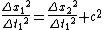
And taking square root we get:

And since 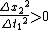 this means: this means:
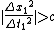
|  |
|
|
Comments |
aaron
2015-11-07 13:34:09 | I was suggested this web site by means of my cousin. I am no longer positive whether this post is written by him as nobody else realize such targeted about my difficulty. You\'re amazing! Thanks!\r\nAaron http://www.asko68.doslownie.2ap.pl |  | MonaJalilvand
2015-10-06 19:11:59 | well to demand = 0) , results in , results in 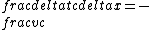 . Since the boost speed is less than c, we have $\\delta x > c \\delta t $.\r\nAlso if you imagine the coordinates system, it is clear that for space like events, they can be placed on the x\' axis. . Since the boost speed is less than c, we have $\\delta x > c \\delta t $.\r\nAlso if you imagine the coordinates system, it is clear that for space like events, they can be placed on the x\' axis. |  | kaic
2013-10-08 00:31:10 | Here's a simple conceptual way to look at this problem. rnrnFirst, draws a simple 2D diagram of a lightcone ( vs vs  , with , with  = | = | | corresponding to the lightcone), the events which lie inside the cone are "timelike separated" or causally connected, because a signal from one event could reach the other. Because of their causal relation, all observer MUST agree on the order they happened. rnrnSo, only those events which are connected by a line which goes outside the light cone (with a slope less than the edge of the cone) could possibly be seen to happen at the same time. rnrnIf you recall that Lorentz boosts tilt the plane of simultaneity, defined by | corresponding to the lightcone), the events which lie inside the cone are "timelike separated" or causally connected, because a signal from one event could reach the other. Because of their causal relation, all observer MUST agree on the order they happened. rnrnSo, only those events which are connected by a line which goes outside the light cone (with a slope less than the edge of the cone) could possibly be seen to happen at the same time. rnrnIf you recall that Lorentz boosts tilt the plane of simultaneity, defined by  , then this means that the horizontal line which defines simultaneous events can be rotated such that both events lie on it; but it can't be rotated into the light cone, that would correspond to an observer travelling faster than light (the t-axis which corresponds to the observer's 4-velocity, would be outside the light cone). rnrnThis would be much easier to show with a simple diagram, but hopefully this helps someone. , then this means that the horizontal line which defines simultaneous events can be rotated such that both events lie on it; but it can't be rotated into the light cone, that would correspond to an observer travelling faster than light (the t-axis which corresponds to the observer's 4-velocity, would be outside the light cone). rnrnThis would be much easier to show with a simple diagram, but hopefully this helps someone. |  | walczyk
2011-04-07 07:16:49 | as kentai pointed out, you can quickly set up the scenario the problem is talking about and use lorentz invariance! Don't be confused, y is just x in a different coordinate frame, not along another axis.. 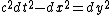 , and we can do , and we can do =dy^2) . Now its kind of apparent.. . Now its kind of apparent..
walczyk
2012-10-07 15:48:12 |
err  and and  = -dy^2)
|
|  | matweiss
2010-11-10 18:23:20 | Here is a more conceptual way to think about it
First, we can throw out A and E since these are ludicrous options to begin with. Also, D is far to specific and one should be able to tell this is incorrect.
This leaves A and B. Think about what this equation implies. dx/dt
looking at dx/dt>c this means that as long as t is not above a certain value the events can appear simultaneous if the observer just travels fast enough (obviously keeping in mind the limit vReply to this comment |  | matweiss
2010-11-10 18:22:43 | Here is a more conceptual way to think about it
First, we can throw out A and E since these are ludicrous options to begin with. Also, D is far to specific and one should be able to tell this is incorrect.
This leaves A and B. Think about what this equation implies. dx/dt
looking at dx/dt>c this means that as long as t is not above a certain value the events can appear simultaneous if the observer just travels fast enough (obviously keeping in mind the limit vReply to this comment |  | sharktopus
2010-10-07 18:46:41 | In this situation we want 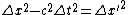 . .
Then we know that 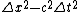 must be positive, so $\Delta x^2 > c^2 \Delta t^2 must be positive, so $\Delta x^2 > c^2 \Delta t^2 \Delta t^2 \Delta t^2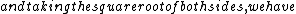 \sqrt{\Delta x^2 / \Delta t^2} = | \Delta x / \Delta t | > c$. \sqrt{\Delta x^2 / \Delta t^2} = | \Delta x / \Delta t | > c$.
sharktopus
2010-10-07 18:53:04 |
In this situation we want 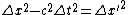 . Then we know that . Then we know that 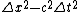 must be positive. must be positive.
Therefore, 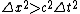 . Dividing by . Dividing by 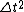 and taking the square root of both sides, we have and taking the square root of both sides, we have
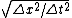 = | = |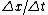 | > c. | > c.
|
|  | thebigshow500
2008-10-12 16:10:18 | Just Check out Griffiths p.502 - "The invariant interval." Everything is super clear there.
Mr. Griffiths derives the result of interval between two events as I = 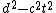
I < 0 refers to timelike interval. Two events occur simultaneously.
I > 0 refers to spacelike interval. Two events occur at the same place.
I = 0 refers to lightike interval. Two events are connected by a signal traveling at c!
For this question, I > 0, so the term 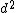 dominates dominates 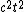 . One can deduct the answer (C)!! . One can deduct the answer (C)!!
thebigshow500
2008-10-12 16:15:53 |
Correction:
I < 0 refers to timelike interval. Two events occur at the same place.
I > 0 refers to spacelike interval. Two events occur simultaneously.
|
thebigshow500
2008-10-12 16:17:15 |
Correction:
I < 0 refers to timelike interval. Two events occur at the same place.
I > 0 refers to spacelike interval. Two events occur simultaneously.
|
goldenkid314
2009-04-02 06:37:27 |
It is actually:
I < 0 refers to timelike interval. Two events occur at the same place and are separated by an interval of time.
I > 0 refers to spacelike interval. Two events occur at the same time and are separated only in space.
The definition you give would lead to answer b) being correct, which it is not.
|
keithpenney
2010-11-12 17:30:05 |
Minor correction: From Griffith's Introduction to Electrodynamics, pg 503
"If I<0 we call this interval timelike, for this is the sign we get when the two occur at the same place (d=0), and are separated only temporally." (in other words, they are NOT simultaneous)
"If I>0 we call the interval spacelike, for this is the sign we get when the two occur at the same time (t=0), and are separated only spatially." (in other words, they occur simultaneously but not at the same place)
And as Yosun said, we want to be in a spacelike interval, because (as Griffith's puts it),
"...if the interval... is spacelike, then there exists a system... in which the two events occur at the same time."
|
amber
2014-10-22 19:04:08 |
Dr Griffiths!
|
theolojest
2016-10-19 04:01:35 |
I think you have them switched but the answer is correct.\r\n\r\n\"If the displacement between two events is time like(I<0), there exists an inertial system in which they occur at the same point.\" -Griffiths 4th ed E&M
|
|  | ivalmian
2008-03-25 19:02:24 | You can also show this through a little math.
We know that for 2 arbitrary reference frames  and and 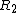 , the time intervals between the two events is: , the time intervals between the two events is:
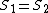
Plugging in  , , 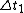 , , 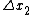 , and , and 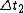 we get: we get:
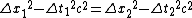
If in 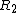 the event is perceived as simultaneous, then the event is perceived as simultaneous, then 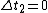 . Thus we get: . Thus we get:

Dividing by 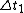 we get: we get:
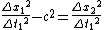
Adding 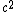 to both sides we get: to both sides we get:
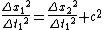
And taking square root we get:

And since 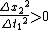 this means: this means:
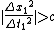
joe35
2008-06-27 14:56:42 |
This is a nice solution. It might help to clarify that  and and 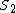 refer to the Lorentz scalar distance, refer to the Lorentz scalar distance, 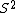 between two events, which is the same in all inertial reference frames. between two events, which is the same in all inertial reference frames.
|
Prologue
2009-10-23 13:27:30 |
This last line 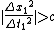 should be should be 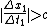 . .
|
Prologue
2009-10-23 13:28:39 |
This last line 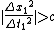 should be should be 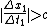 . .
|
Kentai
2009-11-06 14:34:43 |
It is slightly easier then that...
you have dx^2 - (c^2 *dt^2) = dx'^2
factorize dt^2 out from the left hand side, the eqn becomes dt^2 ((dx/dt)^2 - c^2) = dx'^2
it is obvious that dx/dt has to be greater then c in order to get a positive dx'^2
(too lazy to follow the latex syntax...)
|
|  | keflavich
2005-11-10 12:22:03 |  should be squared, I think. You can also remember that for an observer to say that two events happened at the same time, they can't have a causal relationship, and therefore their spatial separation has to be greater than should be squared, I think. You can also remember that for an observer to say that two events happened at the same time, they can't have a causal relationship, and therefore their spatial separation has to be greater than 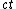 . i.e. . i.e.  if if 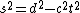 (if you use a Minkowski diagram with time on the y-axis, these signs are correct) (if you use a Minkowski diagram with time on the y-axis, these signs are correct)
yosun
2005-11-10 12:34:06 |
keflavich: thanks for the typo-alert; the typo is now corrected.
i'm planning on posting diagrams sometimes during winter break.meanwhile, here's an open call to other users for submitting diagrams... email them as gif/jpg attachments to yosun(at)nusoy(dot)com.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
