|
GR0177 #32
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
physgre
2015-10-15 08:09:27 | 坑爹啊,m不是动质量吗
PinkieSans
2018-10-23 01:24:01 |
对啊,能量、动量、质量的恒等式里面就是动质量,E^2=p^2*c^2+m^2*c^4并不是m 0
|
|  | neo55378008
2012-03-23 12:05:47 | You may have seen in a relativity course that you can make a right triangle out of rest mass, momentum, and total energy (this comes from the invariance of four-momentum).
Using Pythagorean's formula 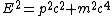
The good thing about the triangle is some times they'll give you numbers for a special triangle (i.e. rest mass of 3, momentum of 4, energy must be 5). Knowing your special triangles could save you some time!
neo55378008
2012-03-23 12:09:47 |
You can also work in units where c=1 just to make things faster
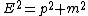
|
|  | QM320
2008-11-05 20:40:21 | In the original solution -- what is  ? ?
p014k
2009-02-15 17:47:42 |
\beta is v/c
|
|  | joshuacc1
2005-12-02 23:50:42 | There\'s a simpler way to answer this question...
E^2 = (pc)^2 + (mc^2)^2
E = 2mc^2 = sqrt((pc)^2 + (mc^2)^2)
4(mc^2)^2 = (pc)^2 + (mc^2)^2
3(mc^2)^2 = (pc)^2
pc = sqrt(3)mc^2
choice (D)
Walter
2008-08-15 16:22:27 |
This is a great solution, I've just laid it out again..
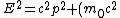^{2})
The question says the total energy is twice the rest energy, which gives
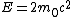
square that
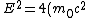^2)
Equating the two expressions for 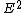 gives gives
^2 = c^{2}p^{2} +( m_{0}c^{2})^{2})
make 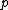 the subject and you get the subject and you get  , answer D as required, and you never even went near a , answer D as required, and you never even went near a 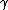 , and that's got to be a good thing. , and that's got to be a good thing.
|
istezamer
2009-11-01 15:09:48 |
lovely!! I solved it this way!! thanks! :D
|
testtest
2010-11-06 16:31:13 |
Even easier if you take c=1 :
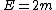

or
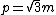
just put the c back to get the answer.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
