GREPhysics.NET: GR0177 #25

GR0177 #25

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Mechanics $\Rightarrow$ }Moment of Inertia

The moment of inertia of the center penny about the center is just 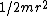$1/2 m r^2$

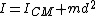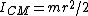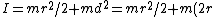The moment of inertia of any one of the other pennis about the center is given by the parallel axis theorem, $I=I_{CM} + md^2$ , where d is the distance from the new point from the center of mass. $I_{CM}=mr^2/2$ for each penny, and thus one has $I=mr^2/2+md^2=mr^2/2+m(2r)^2=9/2mr^2$ , since the distance from the center of each penny to the center of the configuration is 2r.

Since there are 6 pennies on the outside, one has the total inertia 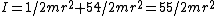$I=1/2mr^2+54/2mr^2=55/2mr^2$ , as in choice (E).

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

gmlaghari85
2014-08-13 00:49:34

Make it simple. Take any diagonal..

I = Icm + md^2= 1/2 mr^2 + Md^2 where M=3m on diagonal and d = 3r
then I = 1/2 mr^2 + 72mr^2 = 55/2 mr^2

gmlaghari85
2014-08-13 00:51:15

sorry its 27mr^2

Ac31415
2017-08-31 16:08:17

I understand this method. But why does it work??

Reply to this comment

physik
2011-04-07 11:22:50

whats wrong with just doing this:rnrnIp:=I for the 6 penniesrnrnIp=6*(Mr^2)/2rnwe conclude that r=3R because thats how far each disk's boundery is from the center of the systemrn=> Ip= 6 $\frac{M}{2}$ *(3R)^2rn=> Ip= 6*(9) $\frac{M}{R^2}$ /2rnso Ip=(54/2)MR^2rnrnNow the center penny is just one disk Icp= (1/2)MR^2rnrnTotal I = Ip + Icp = (55/2)MR^2 Choice Ern

physik
2011-04-07 16:24:34

Im sorry about the look of this thing.
What I wanted to write was moment of inertia for the 6 disks is
Ip=6*(MR^2)/2

here R =3r => R^2 = 9r^2
Ip=((6*9)/2) Mr^2

and the moment of inertia of the central disk is Icp=MR^2/2

Total moment I = (MR^2)/2 + (54/2)(MR^2)

Reply to this comment

anmuhich
2009-03-14 10:35:10

A faster way to do this is to treat the whole configuration as a disk and approximate the moment of intertia:

I=(1/2)(M)(R*R)

M= 7m and R= 3r

This gives I=(56/2)m *r*r which makes sense because this answer should be a little over the actual answer which is now obviously E

f4hy
2009-04-02 15:08:03

I wish I thought of that. Thanks.

mr_eggs
2009-08-16 21:23:26

but 9*7 is 63...

bcomnes
2011-09-22 16:11:53

It is an interesting way to get a ballpark number, but the number you actually get will not make sense if the answer choices include numbers between what this method gets and the actual correct answer.

Reply to this comment

Post A Comment!

You are replying to:

A faster way to do this is to treat the whole configuration as a disk and approximate the moment of intertia: I=(1/2)(M)(R*R) M= 7m and R= 3r This gives I=(56/2)m *r*r which makes sense because this answer should be a little over the actual answer which is now obviously E

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone