|
GR0177 #26
|
|
|
|
|
Alternate Solutions |
kroner
2009-10-05 11:10:58 | It's quicker to consider the motion about the pivot point instead of about the center of mass, since then the linear kinetic energy term drops out (since the pivot point is stationary).
 with with  . The velocity of the end point is . The velocity of the end point is 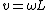 . .
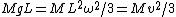
 . . |  | wittensdog
2009-09-13 16:15:22 | So, there's an alternate method I used to solve this problem which makes no reference to moment of inertia at all, which I think is relatively quick and simple.
First, recognize that if we set the potential energy to be zero at the height of the pivot point, we start out with all of the energy as potential energy, and by the time the rod falls over, it is entirely kinetic.
The initial potential energy of an infinitesimal part of the rod is g*h*dm, where h ranges from zero to L. Replacing dm with (M/L)*dh, we get g*(M/L)*h*dh. This is a two second integral which results in (M*g*L)/2 for the total potential energy (the same as if you averaged the energy of a point mass M at height zero and L).
Now, the kinetic energy of an infinitesimal portion of the rod when it is moving is (1/2)*dm*v^2. Again replacing dm with (M/L)*dh, and the velocity with h*w, where w is whatever the angular velocity of the rod is, we have (1/2)*(M/L)*w^2*h^2*dh. Again, this integral takes about two seconds and gives (M*L^2*w^2)/6. Now, if you equate this with the potential energy, and cancel the mass terms and a factor of two, you immediately get,
g*L = (L*w)^2 / 3
from which it is easy to solve for L*w, or the velocity at the end of the rod, and you indeed get answer C. The telling of the method makes it seem long, but it really is only about a 30 second problem at the very most, if you know what to do. |  |
|
|
Comments |
nepo
2016-02-02 18:32:48 | From where did we get E = mg L / 2 ? |  | tweetiebird
2014-11-28 20:32:15 | The author leaves off a L^2 term in one step |  | saforem2
2013-06-26 15:03:27 | I'm confused as to why you have 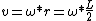 initially, but then when you solve for v in terms of initially, but then when you solve for v in terms of  you use you use 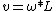 instead of instead of 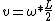 |  | wtf_is_wrong?
2011-06-07 21:48:33 | Is it wrong to simply use  ? Where ? Where 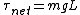 and and  = =  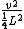 . Which ends up giving you . Which ends up giving you 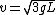 . . |  | his dudeness
2010-09-24 16:11:53 | Fellas! What's with all the fancy formulas? There's a much easier way to do the problem. Imagine we take a mass and drop it from a height L/2. Its potential energy gets converted into potential energy and it hits the ground with velocity  . Now, in our case, the potential energy doesn't get converted purely into kinetic energy, because some of it has to go into rotational energy as well. It's pretty clear that the final velocity of any point on the rod will be less than . Now, in our case, the potential energy doesn't get converted purely into kinetic energy, because some of it has to go into rotational energy as well. It's pretty clear that the final velocity of any point on the rod will be less than  , so answer (A) is the only one that fits. , so answer (A) is the only one that fits.
As always, the lesson about the Physics GRE is: never plug and chug unless you absolutely have to!
his dudeness
2010-10-10 13:14:20 |
Whoah, my original answer was totally off base, please disregard it! (I guess the key here is that the end of the rod is moving twice as fast as the middle of the rod).
In retrospect, it seems like the best solution is conservation of energy about the pivot point. You get:
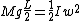 , where , where  . Plug and chug to get the right answer. . Plug and chug to get the right answer.
|
|  | kroner
2009-10-05 11:10:58 | It's quicker to consider the motion about the pivot point instead of about the center of mass, since then the linear kinetic energy term drops out (since the pivot point is stationary).
 with with  . The velocity of the end point is . The velocity of the end point is 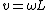 . .
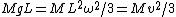
 . .
kroner
2009-10-05 11:25:51 |
If you get hit on the head and forget all the moment of inertia formulas, the basic ones are pretty easy to derive from scratch.
For a rod: 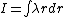 where where  is the linear density, in this case is the linear density, in this case 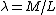 . .
About the center 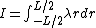 . .
About the end 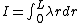 . .
|
kroner
2009-10-05 11:28:41 |
Ha ha, sorry I managed to screw that up. The integrals should be  . I guess I would fail. . I guess I would fail.
|
kiselev
2010-11-02 18:13:28 |
Hi! It says "With what speed does the FREE end of the rod strike the ground?"
This means that your answer must be multiply by 2, so you get (D) \sqr{12gL}
The first solution is just terrible... the center of mass doesnt have translational kinetic energy.
However it seems that ETS made the same mistake and considers that the answer is (C)...Unless they said what is the center of mass velocity when strikes the surface I dont see how this is right
|
aayush3009
2012-09-16 09:23:19 |
On the same lines, i have found a really quick method.
The PE at the top most point of the rod is M.g.L
Now for KE when it hits the ground, consider the rod to be of length 2L and of mass 2M. Now the point of rotation becomes the center of mass of this extended rod. With the new mass and length, MoI, I = (2M)(2L)^2/12. = 2/3 ML^2.
Equate MgL = Iw^2 where w=v/L, you get v = (3gL)^1/2 !!
|
nvp10
2014-04-02 06:21:47 |
Thanks! this is the best solution. Maybe it would also be useful to say why I is what it is: 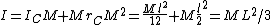 due to the central axis theorem. due to the central axis theorem.
|
nvp10
2014-04-02 06:25:00 |
Sorry, I got the latex wrong. here is what i mean: I=I_{CM}+Mr_{CM}^2=\frac{Ml^2}{12}+M\frac{l}{2}^2=ML^2/3
|
nvp10
2014-04-02 06:26:19 |
and again: 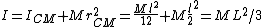
|
RusFortunat
2016-08-11 22:05:48 |
this is a correct solution. disregard OP one
|
NervousWreck
2017-03-28 11:00:04 |
also disregard people trying to find a mistake in this solution. this is the fastest one.
|
|  | wittensdog
2009-09-13 16:15:22 | So, there's an alternate method I used to solve this problem which makes no reference to moment of inertia at all, which I think is relatively quick and simple.
First, recognize that if we set the potential energy to be zero at the height of the pivot point, we start out with all of the energy as potential energy, and by the time the rod falls over, it is entirely kinetic.
The initial potential energy of an infinitesimal part of the rod is g*h*dm, where h ranges from zero to L. Replacing dm with (M/L)*dh, we get g*(M/L)*h*dh. This is a two second integral which results in (M*g*L)/2 for the total potential energy (the same as if you averaged the energy of a point mass M at height zero and L).
Now, the kinetic energy of an infinitesimal portion of the rod when it is moving is (1/2)*dm*v^2. Again replacing dm with (M/L)*dh, and the velocity with h*w, where w is whatever the angular velocity of the rod is, we have (1/2)*(M/L)*w^2*h^2*dh. Again, this integral takes about two seconds and gives (M*L^2*w^2)/6. Now, if you equate this with the potential energy, and cancel the mass terms and a factor of two, you immediately get,
g*L = (L*w)^2 / 3
from which it is easy to solve for L*w, or the velocity at the end of the rod, and you indeed get answer C. The telling of the method makes it seem long, but it really is only about a 30 second problem at the very most, if you know what to do.
wittensdog
2009-10-09 12:56:01 |
Of course, what I'm really doing here in disguise is just deriving the moment of inertia for a rod about one end. Integrals of the form r^2 * dm come up so often in calculations of angular momentum and rotational energy that they were just given their own name as the moment of inertia.
So I guess you can just blindly integrate as in my original method, or integrate to get the moment of inertia of a rod about its end, either way you're pretty much doing the same thing. Or of course you could always just memorize the moment of inertia of a rod about its end.
|
bcomnes
2011-09-22 16:35:28 |
I like this solution a lot. I really need to overcome my aversion dealing with inertia. This way looks long, but it is super simple.
|
|  | AER
2009-04-02 16:23:28 | How do we know there's no force being exerted on the rod by the pivot?
kroner
2009-10-05 11:17:47 |
There is force being exerted on the rod by the pivot. Yosun's solution uses conservation of energy rather than forces.
|
|  | anmuhich
2009-03-14 10:58:08 | For those of us who don't have these mathematical theorem's memorized (like me) and don't want to memorize them, another way to find the moment of inertia for a rod spinning about one end is to take half the moment of inertia of two of the same rods put together spinning about their center. This makes intuitive sense and you could come up with it on your own. So if you work it out:
Irod= (1/2)(1/12) Mnew*Lnew*Lnew
with Mnew=2*M and Lnew= 2*L
plugging in
Irod= (1/2)(1/12)(2M)(4L*L) = 1/3 M*L*L
Then continue with the rest. This way |  | mfidanis1
2009-01-29 16:27:41 | it is called Steiner Theorem.
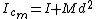 where where 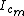 is the moment of inertia of center mass and d the distance between the two axes is the moment of inertia of center mass and d the distance between the two axes |  | michealmas
2006-12-28 16:56:20 | Ok, I don't understand why she is using the
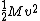
term. The intial potential energy is all transferred to rotational kinetic energy in the final state. Once we get rot. kin. E, THEN we change it to translational energy of the tip of the rod. So:
Use the proper equation for moment of inertia of a rod rotating at its end: ( ) and say: ) and say:

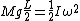
(using 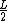 instead of instead of 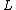 in the LHS because that is the center of mass. This is essentially the in the LHS because that is the center of mass. This is essentially the 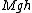 grav. pot. E term from newbie (or 'Yosunist') mechanics.) grav. pot. E term from newbie (or 'Yosunist') mechanics.)
Then plug in  , and solve for , and solve for  to get: to get:
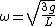
and finish it as Yosun did. |  | senatez
2006-10-29 10:30:53 | I think it is easier to just use parallel axis theorem to derive the moment of inertia around the end of a rod. It will be:
^2 = 1/3 ML^2)
nitin
2006-11-14 01:04:03 |
Well, what Yosun wrote:
=\frac{1}{2}Mv^2+\frac{1}{2}I\omega^2)
actually comes from the so-called parallel-axis theorem. Nevertheless, you're right, and it is much simpler your way.
|
|  | naama99
2006-09-18 20:22:39 | How come the moment of inertia of the rod is I=1/12 MR^2 instead of 1/3 MR^2?
herrphysik
2006-09-22 20:38:51 |
naama99: 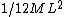 is the moment of inertia of a rod about the center of mass of the rod (axis through the middle), which is what yosun is using in her solution. Granted this problem is much easier and faster to just use is the moment of inertia of a rod about the center of mass of the rod (axis through the middle), which is what yosun is using in her solution. Granted this problem is much easier and faster to just use 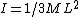 (axis at the end), however ETS doesn't supply this equation on their info sheet, only the first one. But had you the latter memorized, that would be the one to use. Without it though one is forced to use this more involved translational + rotational kinetic energy of the CM business. (axis at the end), however ETS doesn't supply this equation on their info sheet, only the first one. But had you the latter memorized, that would be the one to use. Without it though one is forced to use this more involved translational + rotational kinetic energy of the CM business.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
