GREPhysics.NET: GR0177 #25

GR0177 #25

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Mechanics $\Rightarrow$ }Moment of Inertia

The moment of inertia of the center penny about the center is just 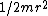$1/2 m r^2$

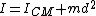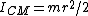The moment of inertia of any one of the other pennis about the center is given by the parallel axis theorem, $I=I_{CM} + md^2$ , where d is the distance from the new point from the center of mass. $I_{CM}=mr^2/2$ for each penny, and thus one has $I=mr^2/2+md^2=mr^2/2+m(2r)^2=9/2mr^2$ , since the distance from the center of each penny to the center of the configuration is 2r.

Since there are 6 pennies on the outside, one has the total inertia 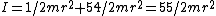$I=1/2mr^2+54/2mr^2=55/2mr^2$ , as in choice (E).

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

anmuhich
2009-03-14 10:35:10

A faster way to do this is to treat the whole configuration as a disk and approximate the moment of intertia:

I=(1/2)(M)(R*R)

M= 7m and R= 3r

This gives I=(56/2)m *r*r which makes sense because this answer should be a little over the actual answer which is now obviously E

f4hy
2009-04-02 15:08:03

I wish I thought of that. Thanks.

mr_eggs
2009-08-16 21:23:26

but 9*7 is 63...

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

<a href="http://www6.shoutmix.com/?grephysics">View shoutbox</a>
ShoutMix chat widget

1GHz Smartphone for 1 cent - best deal on a Samsung Galaxy Phone

Free 3D Virtual World. Largest User-Created Fantasy World. Don't Play, Experience. Join Now!

Bored, got time to kill, and want to earn micro-cash by mindlessly clicking on links? Join CrownGPT. Click Offers. Click the Paid to Click button... then click to your heart's delight.

FREE 3D Virtual World Chat - Join Second Life Today!

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone