|
GR0177 #24
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
johnhero2010
2012-10-08 02:45:31 | Since air resistance is being ignored, there is no force in the horizontal direction. Therefore, the x-component of the particle's velocity is constant. We are told that the stone is thrown in the +x direction. Therefore, the ( v_x) component of the velocity must be positive. Therefore, graph II represents
(v_x) versus (t) . The y-component of the particle's velocity vector is initially positive, but it decreases at a constant rate due to the force of gravity, and eventually becomes negative. Therefore, graph III represents (v_y) versus (t) . Therefore, answer (C) is correct.
|  | secretempire1
2012-08-28 08:13:12 | If you consider just the vertical velocity of the stone, this problem becomes very simple.
You initially toss the stone up, so the y velocity is initially some positive number. This rules out I and V. As gravity acts on the stone, it gets slower and slower and slower until it reaches zero. Then it starts falling, giving it a negative y velocity.
The only graph that represents this behavior is III. And only choice C offers graph III as the choice for the y velocity. |  | isentropic
2008-10-17 08:24:26 | You could also plot the parabolic trajectory of the stone on an xy-plane and draw the velocity components. From there, it should be pretty easy to determine what the vt-graphs should look like. |  | antithesis
2007-10-01 11:54:01 | Actually, in this case, if you only look at 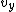 , and realize it is case III, the only answer is (C), and you don't even need to consider , and realize it is case III, the only answer is (C), and you don't even need to consider 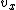 |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
