|
GR9677 #9
|
|
|
|
|
Alternate Solutions |
hamood
2007-04-07 15:24:52 | yeah it makes more sense to go for the smallest Energies (meaning longest wavelengthhs); so n= 2 & 1 for Lyman and n = 3 & 2 for Balmer. |  | senatez
2006-11-01 10:51:41 | Yes, it should be ![[1/(1/1^2-1/2^2]/[1/(1/2^2-1/3^2)] = 5/27](/cgi-bin/mimetex.cgi?[1/(1/1^2-1/2^2]/[1/(1/2^2-1/3^2)] = 5/27) |  |
|
|
Comments |
sina2
2013-09-21 09:37:53 | We should consider:
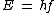 or or
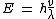
So the longest wavelength belongs to lowest possible energy.
5/27 is correct. |  | nontradish
2012-04-06 20:34:20 | There is roughly a 4 to 1 ratio from Balmer to the Lyman series as quoted in this paper, "This is possible because of the near four to one ratio in wavelengths of Balmer and Lyman." http://www.ph.unimelb.edu.au/~chantler/opticshome/xrayopt/LamingChantlerNIM.pdf
Thanks for this site Yosun!!!
|  | hamood
2007-04-07 15:24:52 | yeah it makes more sense to go for the smallest Energies (meaning longest wavelengthhs); so n= 2 & 1 for Lyman and n = 3 & 2 for Balmer. |  | senatez
2006-11-01 10:51:41 | Yes, it should be ![[1/(1/1^2-1/2^2]/[1/(1/2^2-1/3^2)] = 5/27](/cgi-bin/mimetex.cgi?[1/(1/1^2-1/2^2]/[1/(1/2^2-1/3^2)] = 5/27)
cartonn30gel
2011-04-03 21:45:14 |
5/27 is correct
|
|  | sblusk
2006-10-24 06:10:41 | The ratio of longest wavelengths corresponds to the smallest energy difference. So, one should not use n_i = infinite, but rather
n_i = 2 and 3 for Lyman and Balmer series, respectively. In this case one obtains exactly 5/27. |  | kevglynn
2006-10-22 11:20:24 | I just want to go along with what was mentioned in the last post. For lamda to be a maximum, one would want to minimize its inverse. Therefore, n_i approaching infinity is a wrong assumption. Instead, use the smallest possible value of n_i, which would be n_i = n_f + 1 |  | daschaich
2005-11-07 23:20:46 | Actually, the longest wavelength results when 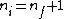 and the shortest wavelength when and the shortest wavelength when 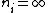 . The result . The result 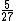 given in A is exact. given in A is exact. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
