GREPhysics.NET: GR9677 #59

GR9677 #59

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Quantum Mechanics $\Rightarrow$ }Laser

Not much understanding of lasers is required to solve this one; the basic idea of the problem tests the relation between photon energy and energy from the laser. Recalling the equation $E=hf=hc/\lambda\approx 12E-7/600E-9=2 eV$ , equates that to the energy (in eV) calculated from $Pt = 10E3 \times 1E-15/1.602E-19$ . The answer comes out to choice (B).

Alternate Solutions

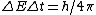
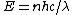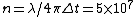
insertphyspun 2011-05-26 13:46:20	Of course, the E=Pt approach is probably best, but I was going too fast to see that P=10kW. My alternate solution uses the uncertainty principle: $\Delta E \Delta t = h/4\pi$ where $E=nhc/\lambda$ . Thus, $n = \lambda/4\pi \Delta t = 5 \times 10^7$ Close enough, and no need to convert Watts to eV/s. Reply to this comment
proctort 2009-09-10 20:00:28	First time posting, defaults to NEC apparently. This one is properly labeled: Given that this answer is virtually illegible, I'm writing out my own answer: The energy of a beam of light is 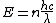$E = n \frac{h c}{\lambda}$ , where $n$ is the number of photons and $\lambda$ is the wavelength. 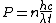As power is defined as P=\frac{E}{t}, where $t$ is the time over which energy is given off, we have $P=n \frac{h c }{\lambda t}$ , which, solving for $n$ gives n = \frac{P \lambda t}{h c}. 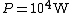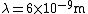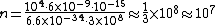In SI units, $P = 10^4 \mathrm{W}$ , $\lambda = 6 \times 10^{-9} \mathrm{m}$ ..., which gives $n = \frac{10^4 \cdot 6 \times 10^{-9} \cdot 10^{-15}}{6.6 \times 10^{-34} \cdot 3 \times 10^8} \approx \frac{1}{3}\times 10^8 \approx 10^7$ Reply to this comment

Comments

digitalhikes
2019-07-08 11:04:17

Happy to go to your post, i\\\\\\\'m by all accounts forward to more and more dependable articles and that i figure we have a tendency to as a full would like to convey such Brobdingnagian numbers of excellent articles, post like Hostpapa Promo Code 2019 to important to us. \\\\r\\\\n

Reply to this comment

insertphyspun
2011-05-26 13:46:20

Of course, the E=Pt approach is probably best, but I was going too fast to see that P=10kW. My alternate solution uses the uncertainty principle:

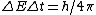
$\Delta E \Delta t = h/4\pi$

where 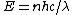$E=nhc/\lambda$ . Thus,

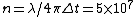
$n = \lambda/4\pi \Delta t = 5 \times 10^7$

Close enough, and no need to convert Watts to eV/s.

Setareh
2011-10-07 09:52:25

I think in this case you have forgotten "c" in denominator of n=lambda/4*pi*t. rnActually the real equation for n is:rnn=lambda/4*pi*c*trnif you put c= 3*10^8 , you will see that it is larger than the correct answer.rnI think you have to write: n<=lambda/4*pi*c*trnyou have only found the boundary, but the power will determine which n is eligible for this problem.

Reply to this comment

proctort
2009-09-10 20:00:28

First time posting, defaults to NEC apparently. This one is properly labeled:

Given that this answer is virtually illegible, I'm writing out my own answer:

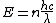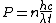The energy of a beam of light is $E = n \frac{h c}{\lambda}$ , where $n$ is the number of photons and $\lambda$ is the wavelength. As power is defined as P=\frac{E}{t}, where $t$ is the time over which energy is given off, we have $P=n \frac{h c }{\lambda t}$ , which, solving for $n$ gives n = \frac{P \lambda t}{h c}.

In SI units, 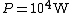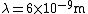$P = 10^4 \mathrm{W}$ , $\lambda = 6 \times 10^{-9} \mathrm{m}$ ..., which gives
$n = \frac{10^4 \cdot 6 \times 10^{-9} \cdot 10^{-15}}{6.6 \times 10^{-34} \cdot 3 \times 10^8} \approx \frac{1}{3}\times 10^8 \approx 10^7$

alisonsparkles
2012-10-02 01:57:42

Doesn't the wavelength = 600*10^-9? This gives me an answer of 1/3*10^10...

calcuttj
2014-09-20 07:21:37

Technically the wavelength is 6E-7 or 600E-9

Reply to this comment

proctort
2009-09-10 19:53:33

Given that this answer is virtually illegible, I'm writing out my own answer:

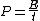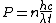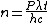The energy of a beam of light is $E = n \frac{h c}{\lambda}$ , where $n$ is the number of photons and $\lambda$ is the wavelength. As power is defined as $P=\frac{E}{t}$ , where $t$ is the time over which energy is given off, we have $P=n \frac{h c }{\lambda t}$ , which, solving for $n$ gives $n = \frac{P \lambda t}{h c}$ .

In SI units, 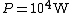$P = 10^4 \mathrm{W}$ , $\lambda = 6 ^{-9} \mathrm{m}$ ..., which gives
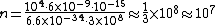$n = \frac{10^4 \cdot 6 \times 10^{-9} \cdot 10^{-15}}{6.6 \times 10^{-34} \cdot 3 \times 10^8} \approx \frac{1}{3}\times 10^8 \approx 10^7$

Reply to this comment

isina
2008-10-18 13:17:55

where does that 1.602E-19 come from?

akbar5223
2008-10-28 08:12:41

The laser power is given in W=J/s, so it is necessary to convert the power from J/s to eV/s, where 1 eV = 1.602E-19 J.

naroays
2008-11-03 02:41:15

Why should we convert to eV/s?

The SI unit of energy is Joules, and 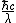$\frac{\hbar c}{\lambda}$ is in Joules, as is Power*time, because it's Joules/second * second = Joules

naroays
2008-11-03 02:51:08

Ah, I just noticed the soln in the website doesn't use SI units. Nevermind

Reply to this comment

Post A Comment!

You are replying to:

Of course, the E=Pt approach is probably best, but I was going too fast to see that P=10kW. My alternate solution uses the uncertainty principle: $\Delta E \Delta t = h/4\pi$ where $E=nhc/\lambda$ . Thus, $n = \lambda/4\pi \Delta t = 5 \times 10^7$ Close enough, and no need to convert Watts to eV/s.

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone