GREPhysics.NET: GR9677 #40

GR9677 #40

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Quantum Mechanics $\Rightarrow$ }Bohr Theory

It's amazing how far one can get with the Bohr formula.

To start with, one should calculate the ground-state energy of the singly ionized Helium (i.e., the ionization energy). $E_1 = Z^2 E_{H1} = 4 \times 13.6 eV$ , since Helium has 2 protons. (The general formula is $E_n = Z^2/n^2 E_1$ .)

The Bohr formula gives $E=E_1\left(1/n_f^2-1/n_i^2\right)=E_1(1/n_f^2-1/16)$ , since $n_i^2=4^2=16$ .

$E=hc/\lambda\approx 1.24E-6/4.7E-7$ gives $E\approx 2.5$ eV.

The only unknown expression above is $n_f$ . Plugging everything in and solving for that, $n_f^{-2}\approx 8^{-1} \Rightarrow n_f\approx 3$ . This yields choice (A). One can check via $E_f=E_1/n_f^2 4\times 13.6/9 \approx 6$ , which verifies (A).

Alternate Solutions

BerkeleyEric 2010-09-22 22:36:21	I think process of elimination is fastest here. From the Bohr formula we know that the n=1 is at 4*(-13.6 eV) ~ -52 eV. So it can't be (D). And it also can't be (B) since the n=2 state wouldn't be all the way up at -6 eV. Now remember that 470 nm falls in the visible regime, so the energy difference must be at around 1-2 eV. This immediately eliminates (C) and (E) since they must be more than this amount lower than the n=4 state. Reply to this comment
archard 2010-07-15 13:50:25	You can also get it with the Rydberg formula, since you're given the wavelength of the photon and the initial energy level. Then it's just plug and chug. Reply to this comment

Comments

cczako
2013-10-18 15:21:38

The way I did was to just remember that E is proportional to Z^2/n^2. Its quick and easy to calculate that n=4 --> E=- 3 eV, n=3 --> E=-6 eV, n=2 --> E=-13.6 eV, and n=1 --> E=-50 eV. This automatically eliminates B and D. Then using the equation E=(hc)/lambda (I always use 1240 nm*eV for hc) you get that 470 nm is about 3 eV. So n=4 of energy -3 eV minus 3 eV gives you -6 eV. This gives you choice A.

Reply to this comment

BerkeleyEric
2010-09-22 22:36:21

I think process of elimination is fastest here. From the Bohr formula we know that the n=1 is at 4*(-13.6 eV) ~ -52 eV. So it can't be (D). And it also can't be (B) since the n=2 state wouldn't be all the way up at -6 eV.

Now remember that 470 nm falls in the visible regime, so the energy difference must be at around 1-2 eV. This immediately eliminates (C) and (E) since they must be more than this amount lower than the n=4 state.

Reply to this comment

archard
2010-07-15 13:50:25

You can also get it with the Rydberg formula, since you're given the wavelength of the photon and the initial energy level. Then it's just plug and chug.

sina2
2013-09-24 02:17:02

I tried in this way, but I failed.

nasim
2015-10-12 17:05:01

One should first have the Rydberg constant to be able to use Rydberg formula! But doesn\'t!

Reply to this comment

asdfman
2009-11-05 00:37:16

You can quickly narrow this down as anything less than ~400 nm is UV. If you remember that 13.6 eV, from hydrogen yields UV then that tosses out choices C, D, and E.

Reply to this comment

f4hy
2009-10-25 19:28:33

I am confused. When finding 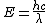$E = \frac{hc}{\lambda}$ are you using the speed of light in cm but the wave length in meters?

kroner
2009-10-29 14:13:19

Everything is in meters there.
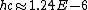$hc \approx 1.24E-6$ eV m or 1240 eV nm,
which good value to know off-hand for problems like this.

Reply to this comment

astro_allison
2005-12-08 22:50:07

don't you mean 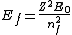$E_{f} = \frac{Z^2 E_{0}}{n_{f}^2}$ ?

Reply to this comment

Post A Comment!

You are replying to:

You can quickly narrow this down as anything less than ~400 nm is UV. If you remember that 13.6 eV, from hydrogen yields UV then that tosses out choices C, D, and E.

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone