|
GR9277 #11
|
|
|
|
|
Alternate Solutions |
niux
2009-11-06 07:02:08 | My way was:
As Q is proportional to 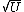 , then you will need a factor of ( , then you will need a factor of (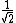 ) for Q (that is, a factor of ) for Q (that is, a factor of 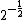 ) in order to obtain ) in order to obtain 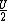 as the problem requires. Then just equate this to time dependece for discharge: as the problem requires. Then just equate this to time dependece for discharge:
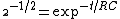
and solving for t, you will get answer (E)
|  | QM320
2008-11-08 06:07:58 | You can also remember (or derive) }) . So . So }) . Squaring this, and using . Squaring this, and using 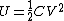 , we find , we find }) . Plug in . Plug in 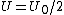 and solve. Voila! and solve. Voila! |  | QM320
2008-11-08 06:07:16 | You can also remember (or derive) }. So ) V=V_0 e^-{t/(RC)} V=V_0 e^-{t/(RC)} U=\frac{1}{2}C V^2 U=\frac{1}{2}C V^2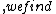 U=U_0 e^{-2t/(RC)} U=U_0 e^{-2t/(RC)} U=U_0/2$ and solve. Voila! U=U_0/2$ and solve. Voila! |  |
|
|
Comments |
psychonautQQ
2013-10-07 14:07:40 | What am I doing wrong..?
Qf = Qie^(t/rc)
U --> Q^2
so Qf^2 = (Qi^2)/(2^2 )--> (Qi^2)/4 = (Qi^2)e^(2t/rc)
1/4 = e^(t/rc)
ln(1/4) = t/rc
rc*ln(1/4) = t.
I realize this is wrong, I feel like the given answer skips some steps, it'd be coo if someone could elaborate.
|  | kstephe6
2012-11-04 17:30:56 | ONLY FAST ANSWERS MATTER!
half life (of charger in this case) is ln(2)*(tau)
this gives the time it takes for (1/2) of the charge to remain, which is the same (by the energy equation) as (1/4) of the energy to remain.
Well, you want twice as much energy left as this, so you only want half of this time to pass. Just the divide the half life by 2.
DONE!
kstephe6
2012-11-05 05:09:16 |
I meant this as an alternate solution.
|
|  | Quark
2011-10-25 13:40:35 | What if instead of U=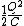 you remembered U= you remembered U=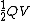 . Then you would think that the energy was proportional to Q instead of . Then you would think that the energy was proportional to Q instead of 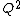 and get the wrong answer... and get the wrong answer...
Dr. D.R. Dopetec
2011-10-31 20:44:52 |
Realize that the charge is constant in this circuit, but the voltage across the capacitor is not. There is no voltage pump (e.g. battery) in this circuit.
|
|  | niux
2009-11-06 07:02:08 | My way was:
As Q is proportional to 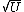 , then you will need a factor of ( , then you will need a factor of (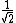 ) for Q (that is, a factor of ) for Q (that is, a factor of 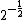 ) in order to obtain ) in order to obtain 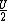 as the problem requires. Then just equate this to time dependece for discharge: as the problem requires. Then just equate this to time dependece for discharge:
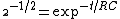
and solving for t, you will get answer (E)
|  | tsharky87
2009-10-30 09:30:42 | In the official solution, he uses Ohm's law as
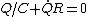 , ,
but isn't Ohm's law actually
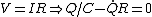 ? ?
kroner
2009-11-01 16:16:31 |
Yosun is implicitly using Kirchhoff's voltage law here: 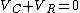 . .
Then from 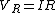 and and 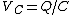 , we get , we get 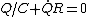 . .
|
|  | QM320
2008-11-08 06:07:58 | You can also remember (or derive) }) . So . So }) . Squaring this, and using . Squaring this, and using 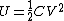 , we find , we find }) . Plug in . Plug in 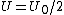 and solve. Voila! and solve. Voila!
gravity
2010-11-07 23:06:46 |
If you're like me and get retarded wondering if it should be divide by two or multiplied by two (debating between Answer D or E), remember that the Energy is proportional to the voltage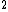 and so the energy will dissipate faster than the voltage, and thus current. The time constant is the time that it takes for the current to half, so we know it should be shorter than this. D is out, E is in. and so the energy will dissipate faster than the voltage, and thus current. The time constant is the time that it takes for the current to half, so we know it should be shorter than this. D is out, E is in.
And that's how you pass the GRE by being too dumb to figure out the U = U /2 stuff. (I don't know, it takes me longer to think about that than it does to think about the answer I gave). /2 stuff. (I don't know, it takes me longer to think about that than it does to think about the answer I gave).
|
|  | QM320
2008-11-08 06:07:50 | You can also remember (or derive) }) . So . So }) . Squaring this, and using . Squaring this, and using 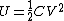 , we find , we find }) . Plug in . Plug in 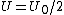 and solve. Voila! and solve. Voila! |  | QM320
2008-11-08 06:07:16 | You can also remember (or derive) }. So ) V=V_0 e^-{t/(RC)} V=V_0 e^-{t/(RC)} U=\frac{1}{2}C V^2 U=\frac{1}{2}C V^2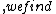 U=U_0 e^{-2t/(RC)} U=U_0 e^{-2t/(RC)} U=U_0/2$ and solve. Voila! U=U_0/2$ and solve. Voila!
QM320
2008-11-08 06:08:38 |
Oops -- bad LaTeX. See the version above!
|
|  | dcb
2007-09-16 14:18:22 | (I'm no expert, so feel free to poke holes in my method).
Mathless solution:
If you can recall these two simple things from your electronics or basic physics class:
1) Time constant for full charge is RC
2) Time relation is logarithmic.
By 1, we can rule out anything greater than RC (eliminate D).
By 2, we can rule out anything without an "ln" (eliminate A, B, C)
That leaves E.
ewhite2
2007-10-27 10:57:35 |
RC is the time to dissipate 2/3 of the charge in the capacitor, not the full charge. However even after putting this value into your line of reasoning it still works for a quick way to find a solution under the time constraints.
|
|  | boundforthefloor
2006-11-19 17:51:50 | The problem asks for the time it takes to lose half of the initial stored energy.
I'd rather think of the equation to solve as ^2 = C*e^(-2t/RC) = 1/2)
which will multiply U by 1/2 as shown in the first equation because C is constant. |  | agaliarept
2006-11-18 15:26:46 | What do you mean by "dissipate by 2"? I am trying to write out the whole equation and something isnt coming out quite right.
StrangeQuark
2007-05-22 12:46:13 |
Try this,
we are looking for the time in which the energy is half of the intial, i.e.
![\frac{U_0}{2}=U[t]](/cgi-bin/mimetex.cgi?\frac{U_0}{2}=U[t])
![\frac{Q_0^2}{2C}\frac{1}{2}=\frac{Q[t]^2}{2C}](/cgi-bin/mimetex.cgi?\frac{Q_0^2}{2C}\frac{1}{2}=\frac{Q[t]^2}{2C})
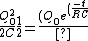})^2}{2C})
Now just solve for t
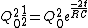
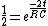
![ln[1]-ln[2]==\frac{-2t}{RC}](/cgi-bin/mimetex.cgi?ln[1]-ln[2]==\frac{-2t}{RC})
![ln[2]RC==2t](/cgi-bin/mimetex.cgi?ln[2]RC==2t)
![t==\frac{ln[2]RC}{2}](/cgi-bin/mimetex.cgi?t==\frac{ln[2]RC}{2})
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
