|
GR0177 #36
|
|
|
|
|
Alternate Solutions |
NervousWreck
2017-03-28 17:21:16 | The most straitforward is to draw a PV diagram where an adiabatic expansion would be a curve, which is steeper than an isoterm. Therefore one immediately notices that the E is False. |  | Ning Bao
2008-02-01 06:29:07 | You could also remember that adiabatic and isothermal are not synonyms -> E.
calcuttj
2014-09-25 04:57:41 |
mariav: An adiabat is a process in which net heat transfer is zero, and if work is done by or onto the gas, the internal energy will change. Remember that internal energy is dependent on T (or vice versa).
For an Isotherm:  U = 0 since T = 0 (and thus Q = W)
For an adiabat: U = -W (and it's expanding so some work must be done by or onto the system).
Thus U != 0 and T != 0
|
| |
|
|
Comments |
shawnjasper
2018-10-18 05:58:06 | Excellent post. This is a very good blog that I will definitively come back to more times this year! Gratitude for helpful post. I am sure this post has helped me save many hours of browsing other related posts just to find what I was looking for. Many thanks! assignment writing services |  | NervousWreck
2017-03-28 17:21:16 | The most straitforward is to draw a PV diagram where an adiabatic expansion would be a curve, which is steeper than an isoterm. Therefore one immediately notices that the E is False. | | nirav_605
2013-10-18 09:27:14 | I don't like how choice C is given.
Its really a matter of definition of work done! Depending on how one defines work, work done by the system or work done on the system, sign can be changed. I usually use
U = Q + W, sooo.... U = W (for me)
W = -  P dV | | anmuhich
2009-03-14 12:57:30 | I agree with Ning Bao. It's easiest just to realize that in an adiabatic process the temperature changes, otherwise it would be isothermal. | | phys2718
2008-09-24 15:58:27 | Careful, zero heat change alone isn't enough to guarantee zero entropy change. For example, in the adiabatic free expansion of the ideal gas there is an increase in entropy. The other necessary condition for no change in entropy is that the process be reversible, which is true here since the problem stated that we have a quasi-static expansion rather than a free expansion | | Ning Bao
2008-02-01 06:29:07 | You could also remember that adiabatic and isothermal are not synonyms -> E.
mariav
2014-09-13 11:13:43 |
But they're not mutually exclusive either.... are they?
|
calcuttj
2014-09-25 04:57:41 |
mariav: An adiabat is a process in which net heat transfer is zero, and if work is done by or onto the gas, the internal energy will change. Remember that internal energy is dependent on T (or vice versa).
For an Isotherm: U = 0 since T = 0 (and thus Q = W)
For an adiabat: U = -W (and it's expanding so some work must be done by or onto the system).
Thus U != 0 and T != 0
|
| | antithesis
2007-10-01 12:19:36 | As a shorter way to do this exists if you remember that for adiabatic process,
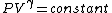
or alternativly,
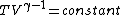
Therefor, if V changes (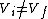 ), T must change, and so (E) can't be true. | |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
