|
GR0177 #3
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Kepler's Third Law }Kepler's Third Law
Recall Kepler's Third Law stated in its most popular form, The square of the period is proportional to the cube of the orbital radius. (Technically, the orbital radius is the semimajor axis of the ellipse.)
Recast that commonsense fact above into equations to get  , as in choice (D). , as in choice (D).
|
|
|
Alternate Solutions |
rifraff
2016-08-06 22:59:29 | (I apologize if this was a double post. The first post was acting funny.)\r\n\r\nIf anyone wants a solution that\'s a bit easier by \"feel,\" maybe:\r\n\r\nThe radial acceleration, a, is proportional to v^2/R.\r\n\r\nThat same radial acceleration is proportional to 1/R^2, since the force is similarly proportioned.\r\n\r\nv^2/R ~ 1/R^2,\r\nso v ~ 1/√R.\r\n\r\nFinally, the time it takes to complete an orbit is t = d/v, where the \"circumference\" d is proportional to R.\r\n\r\nso t ~ R/v, or t ~ R^(3/2).\r\n\r\nThis was easier for me after the first 2 answers were ruled out with some thinking.\r\n\r\nMan, I wish I knew LaTeX. |  | rifraff
2016-08-06 22:58:18 | If anyone wants a solution that\'s a bit easier by \"feel,\" maybe:\r\n\r\nThe radial acceleration, a, is proportional to v^2/R.\r\n\r\nThat same radial acceleration is proportional to 1/R^2, since the force is similarly proportioned.\r\n\r\nv^2/R ~ 1/R^2,\r\nso v ~ 1/√R.\r\n\r\nFinally, the time it takes to complete an orbit is t = d/v, where the \"circumference\" d is proportional to R.\r\n\r\nso t ~ R/v, or t ~ R^(3/2).\r\n\r\nThis was easier for me after the first 2 answers were ruled out with some thinking.\r\n\r\nMan, I wish I knew LaTeX. |  | nathan12343
2008-08-13 13:44:56 | One can always remember that

And, from the Virial Theorem,
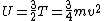
From this we get
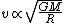
Now, the orbital Period,  , is nothing but , is nothing but
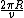
So, we have,
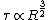
Which is the answer |  |
|
|
Comments |
rifraff
2016-08-06 22:59:29 | (I apologize if this was a double post. The first post was acting funny.)\r\n\r\nIf anyone wants a solution that\'s a bit easier by \"feel,\" maybe:\r\n\r\nThe radial acceleration, a, is proportional to v^2/R.\r\n\r\nThat same radial acceleration is proportional to 1/R^2, since the force is similarly proportioned.\r\n\r\nv^2/R ~ 1/R^2,\r\nso v ~ 1/√R.\r\n\r\nFinally, the time it takes to complete an orbit is t = d/v, where the \"circumference\" d is proportional to R.\r\n\r\nso t ~ R/v, or t ~ R^(3/2).\r\n\r\nThis was easier for me after the first 2 answers were ruled out with some thinking.\r\n\r\nMan, I wish I knew LaTeX. |  | rifraff
2016-08-06 22:58:18 | If anyone wants a solution that\'s a bit easier by \"feel,\" maybe:\r\n\r\nThe radial acceleration, a, is proportional to v^2/R.\r\n\r\nThat same radial acceleration is proportional to 1/R^2, since the force is similarly proportioned.\r\n\r\nv^2/R ~ 1/R^2,\r\nso v ~ 1/√R.\r\n\r\nFinally, the time it takes to complete an orbit is t = d/v, where the \"circumference\" d is proportional to R.\r\n\r\nso t ~ R/v, or t ~ R^(3/2).\r\n\r\nThis was easier for me after the first 2 answers were ruled out with some thinking.\r\n\r\nMan, I wish I knew LaTeX. |  | secretempire1
2012-08-28 06:29:51 | The general velocity equation is 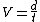 . .
Orbital velocity 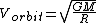 . .
so if you consider your distance in the equation to be the orbital path, then 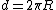 . .
Rearranging the general equation to solve for time leaves 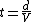 . .
Plugging in yields 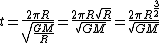 . .
Therefore 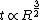 . . |  | nathan12343
2008-08-13 13:44:56 | One can always remember that

And, from the Virial Theorem,
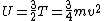
From this we get
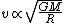
Now, the orbital Period,  , is nothing but , is nothing but
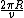
So, we have,
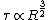
Which is the answer |  | michealmas
2007-01-01 16:00:24 | That's an elegant way to solve it, but if you didn't remember it, you could equate the forces, Newtons Law of Gravitation with the centripetal force for uniform circular motion:
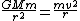
using
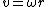
and
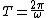 . . |  |
|
| Post A Comment! |
You are replying to:
If anyone wants a solution that\'s a bit easier by \"feel,\" maybe:\r\n\r\nThe radial acceleration, a, is proportional to v^2/R.\r\n\r\nThat same radial acceleration is proportional to 1/R^2, since the force is similarly proportioned.\r\n\r\nv^2/R ~ 1/R^2,\r\nso v ~ 1/√R.\r\n\r\nFinally, the time it takes to complete an orbit is t = d/v, where the \"circumference\" d is proportional to R.\r\n\r\nso t ~ R/v, or t ~ R^(3/2).\r\n\r\nThis was easier for me after the first 2 answers were ruled out with some thinking.\r\n\r\nMan, I wish I knew LaTeX.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
